基金项目:国家科技支撑计划项目课题“基于地震构造分析、综合多学科信息的大地震危险性分析方法研究”(2012BAK19B01-01)专题资助.
(Earthquake Administration of Sichuan Province,Chengdu 610041,Sichuan,China)
Time- and Magnitude- Predictable Model; earthquake recurrence; Sichuan-Yunnan Block; seismic source sections
备注
基金项目:国家科技支撑计划项目课题“基于地震构造分析、综合多学科信息的大地震危险性分析方法研究”(2012BAK19B01-01)专题资助.
根据时间—震级可预报模式研究川滇地块边界断裂系统的地震复发规律,利用历史地震记录和断层滑动速率资料得到了相应的时间可预报统计模型和震级可预报统计模型,并对川滇地块边界断裂带8个震源段在未来10年内的强震复发危险性进行概率评估。计算结果表明,综合危险率K值最高的3个震源段依次为小江断裂带(S5段)、红河、曲江、石屏断裂带(S6段)和安宁河—则木河以及大凉山断裂带(S3段),计算得到这些断裂带下次发生地震的震级分别为7.4、7.1和7.1级; 其中S5、S3段发震位置位于南东边界,S6段位于南西边界,表明未来10年内川滇地块南部边界发震的危险性高于北部边界; 预期的下次发生的最高震级地震位于南东边界。
The law of earthquake recurrence of the fault system in the boundary of Sichuan-Yunnan block is studied based on the Time- and Magnitude- Predictable Model,and the corresponding time- and magnitude- predictable statistical models have been obtained by using the historical earthquake records and the fault slip rate data,then the strong earthquake recurrence probabilities of 8 seismic source sections in the Sichuan-Yunnan block boundary fault zone are assessed in next 10 years. The calculation results show that the 3 seismic source sections of the highest integrated risk rate K are the Xiaojiang Fault Zone(S5 segment),Honghe,Qujiang,Shiping Fault Zones(S6 segment),and Anninghe-Zemuhe,Daliangshan Fault Zones(S3 segment),and the magnitude of the next earthquake occurred on these three subsections are 7.4,7.1 and 7.1 respectively. The S5 and S3 segments are located in the southeast boundary and the S6 segment is located in the southwest boundary,which showed that the reoccurrence risk in southern Sichuan-Yunnan block boundary is higher than that in northern boundary in next 10 years,and the next expected earthquake with maximum magnitude will be occarred in the southeast boundary.
引言
川滇地块(或称川滇菱形块体)是由甘孜—玉树断裂带、鲜水河断裂带、安宁河断裂带、则木河断裂带、小江断裂带、红河断裂带、龙蟠—乔后断裂带和金沙江断裂带等围限的不封闭菱形地块; 它位于青藏高原的东南部,南接巽他地块(张建国等,2014),并相对于外围区域有向南南东方向移动趋势; 其东边界主要断裂带均为左旋错动,西边界断裂带为右旋错动; 此菱形地块控制着中国西南地区的主要地震活动。李坪和汪良谋(1975)在对川滇地区地震地质背景和新构造运动特点研究的基础上首先提出了川滇菱形块体的概念,在此基础上骆佳骥等(2012)开展了应力场分区研究。
川滇地块地震活动频繁,是中国大陆地震活动最强烈的地区之一。据统计,20世纪发生5级以上地震217次,6级以上地震主要沿活动断裂分布,7级以上大震基本分布于块体边缘(皇甫岗等,2007)。
近年来,国内外的研究者探讨了川滇地块及其邻近区域的强震活动规律,并对主要边界断层段强震的发生趋势提出了不同程度的预测,这些研究方法包括:强震活动图像类比(黄圣睦,朱航,2002),川滇菱形块体的东西地区地震活动关联程度(皇甫岗等,2007),库仑应力变化图像(Gkarlaouni et al.,2008),断裂系统的构造动力学与强震序列的关联性(闻学泽等,2011)和利用弹性位错模型反演(程佳等,2011)。
Papazachos(1989)在研究爱琴海及其周围浅源强震的关系后,提出了时间—震级可预报模式。他发现在既包含有较大规模的主断裂、也可能包含有次级断裂的地区,地震的复发有类似于时间、震级可预测的特点,在此基础上给出了地震复发长期预测的统计模型和计算方法。此后的20多年,研究者将时间—震级可预报模式先后应用于全球主要地震活跃区的长期地震预测研究,如爱琴海地区(Papazachos,1992),中美和南美西海岸(Papadimitriou,1993),日本地区(Papazachos,Papaioannou,1994),中美洲和加勒比海地区(Panagiotopoulos,1995),阿尔卑斯—喜马拉雅地区(Papazachos et al.,1997),喜马拉雅中部(Paudyal et al.,2009),喜马拉雅克什米尔地区(Yadav et al.,2010),华北及西南地区(邵辉成,金学申,1999),中国南北地震带(易桂喜,闻学泽,2000)。
川滇地块边界也是由大规模的主断裂及其次级断裂所组成的断裂系统,符合应用地震复发的时间—震级可预报模式的基本构造条件。本研究将根据历史地震记录和断层滑动速率资料,应用时间—震级可预报模式对川滇地块边界断裂不同段落的未来强震复发危险性进行概率评估。
1 研究方法
Papazachos和Papaioannou(1993)基于对爱琴海地区浅源强震之间时间间隔关系的研究结果,提出了区域时间—震级可预报模式的表达式为
lnTt =bMmin+cMp+dlnm0+t,(1)
Mf=BMmin+CMp+Dlnm0+m.(2)
式(1)和(2)是两个多元回归方程。其中,Tt为强震时间间隔,Mp和Mf 分别为上次和下次主震的震级,Mmin是统计中所用的最小震级,m0是该震源区的地震矩年变化率,b、c、d、t、B、C、D和m为回归常数。
在式(1)和(2)中,m0作为地震活动水平的量度,表征震源区的应力积累状态。该模型与其它强震复发模型的主要差别在于把强震重复性与应力积累状态联系起来,因此具有明确的物理意义。
Papazachos(1993)在计算地震矩年变化率m0时,采用Molnar(1979)在G-R关系的基础上建立的计算公式
m0=G/(1-E)×M(1-E)0,max.(3)
式中,G=10(a+bk/r),E=b/r,M0,max是一个震源区最大震级地震所释放的矩,a,b为震级—频度关系式 lnN=a-bM中的常数,r,k则为地震矩M0与震级M经验关系式lnM0=rM+k中的常数。
确定一个震源区的a、b参数值,需要长时间、较完整的地震记录资料,而本文研究区在20世纪70年代以后才建起较为完善的地震观测台网。在过去发表的研究结果中,普遍存在用较短时间的地震资料去倒推过去较长时间内的地震活动的情况,这可能会导致仅仅使用了部分平静期或活跃期的资料而掩盖了长期地震活动的真实情况,从而使所求得的地震矩速率可能与实际不符(易桂喜,1998)。
为了解决这一问题,本文提出使用断层长期平均滑动速率计算地震矩年变化率的方法。1个地震释放的地震矩的表达式为
M0 =μ×D×S.(4)
式中,μ为断层物质之刚性系数,一般为30×109 Pa; D为断层之平均滑动量; S为断层破裂面积。
如果已知1个断层段的年平均滑动速率V,那么该断层段的地震矩年变化率为
m0=μ×V×S=μ×V×L×W.(5)
式中,L为该段断层的长度; W为断层面宽度,在川滇地块一般取15 km。在时间—震级可预报模式中,地震矩年变化率m0是断层段地震活动水平的量度,应该是单位时间、单位断层长度释放的地震矩,它与断层段的年平均滑动速率V正相关,因此本研究在各震源段中,均将L值取为单位长度。
由此,可将式(1)、(2)改写为下列多元回归方程:
lnTt=bMmin+cMp+dlnV+t',(6)
Mf=BMmin+CMp+DlnV+m'.(7)
式中,t'和m'是常数。
2 川滇地块边界震源段的划分
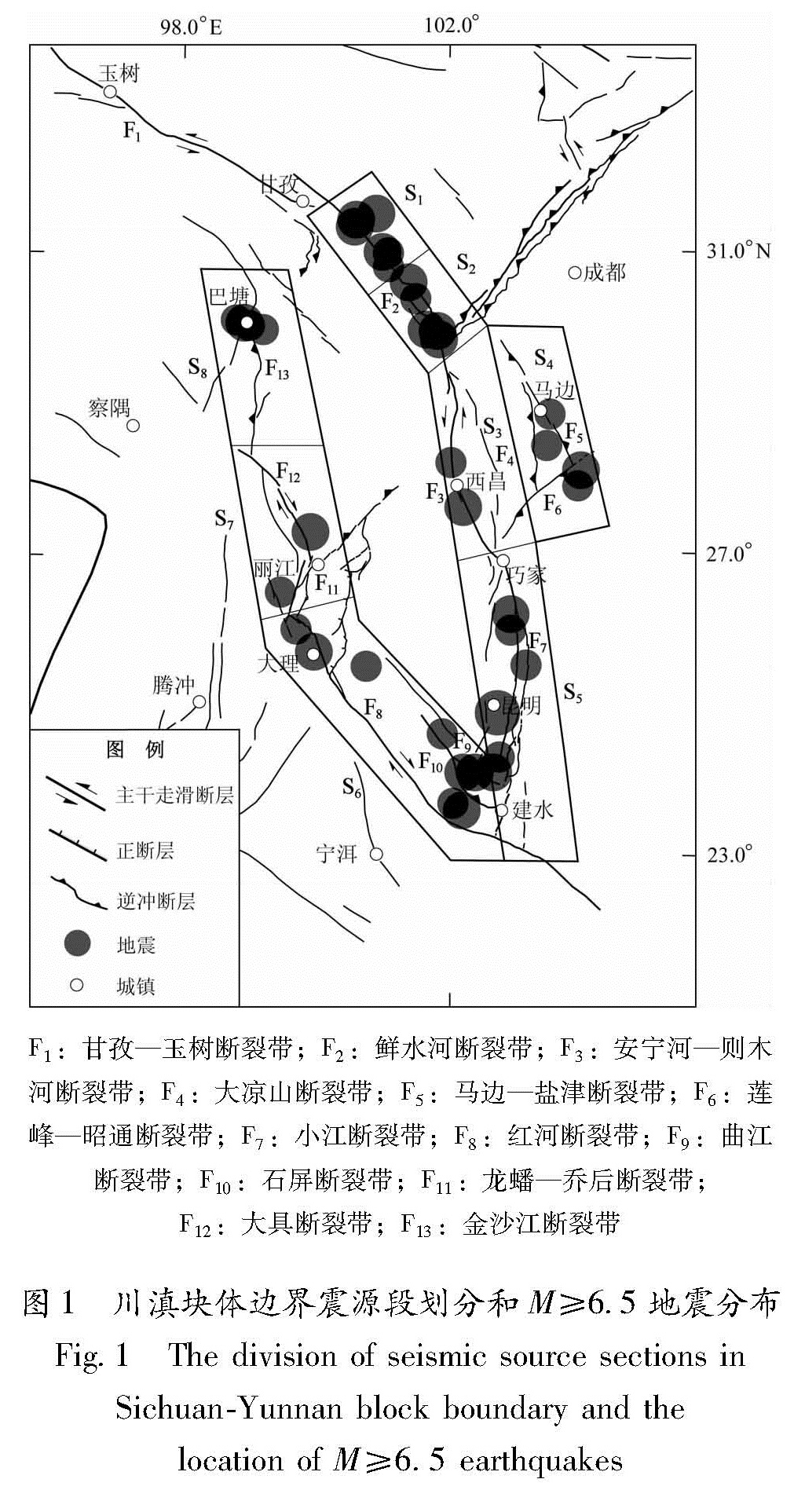
笔者依据构造特征以及地震空间分布的丛集特征,把川滇地块的边界断裂带划分为8个震源段(图1)。北东边界的鲜水河断裂带被分为S1和S2两段; 东边界的安宁河—则木河以及大凉山断裂带为S3段; 与S3段相毗邻的马边—盐津断裂带和莲峰、昭通断裂带作为川滇地块的共同东边界,被称为S4段; 往南的小江断裂带为S5段。川滇地块的西边界被划分为3段,红河断裂带以及曲江、石屏断裂带为S6段,金沙江断裂带为S8段,两段之间的龙蟠—乔后、大具断裂带为S7段。
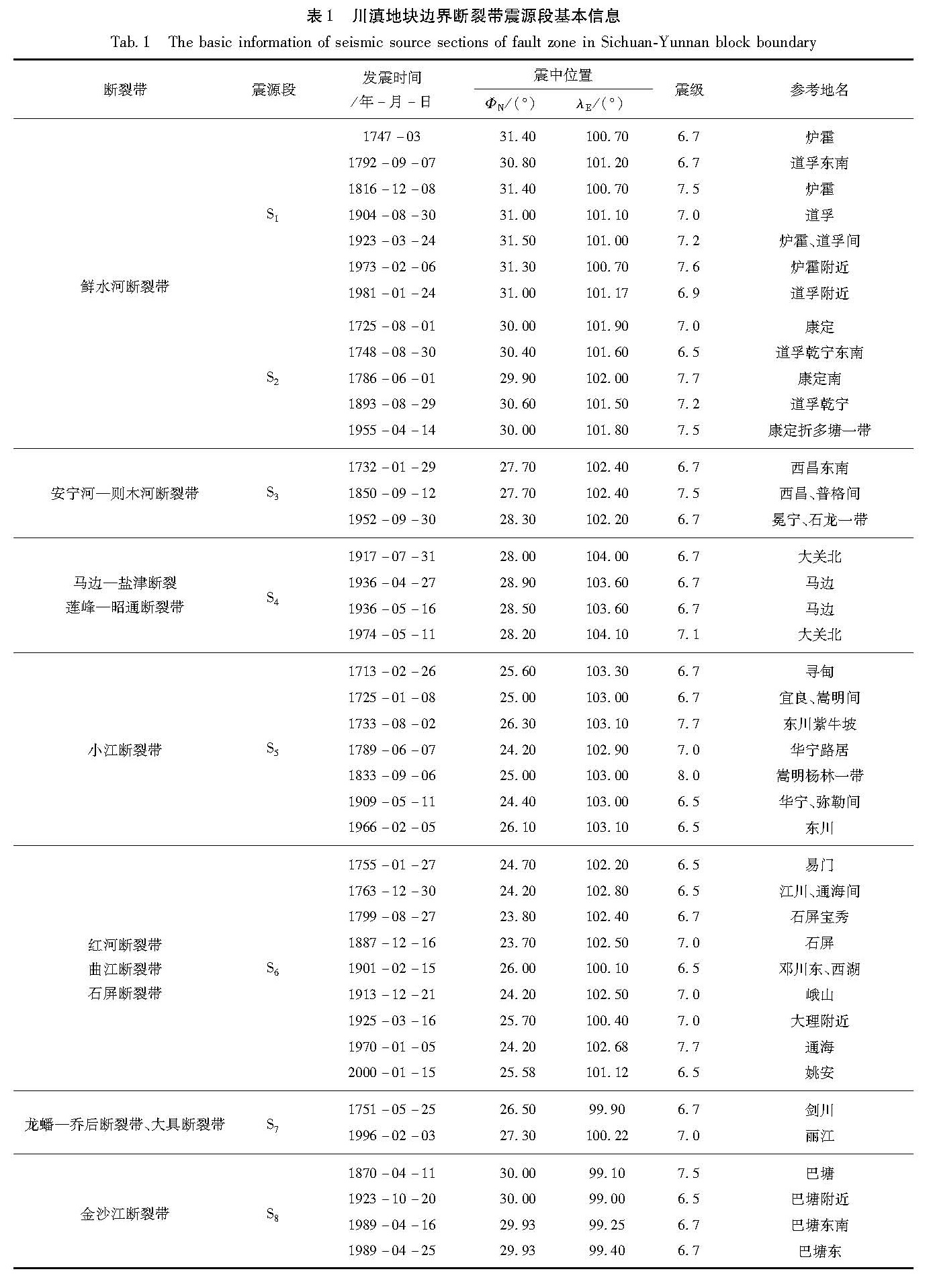
对上述8个震源段内发生的地震,考虑历史记载的完整性,选取1700年以来该区6.5级以上的地震共计41次(表1),地震目录选自《中国强地震目录》 中国地震局监测预报司预报管理处.2010.中国强地震目录(公元前23世纪—2010年5月).。
表1 川滇地块边界断裂带震源段基本信息
Tab.1 The basic information of seismic source sections of fault zone in Sichuan-Yunnan block boundaryF1:甘孜—玉树断裂带; F2:鲜水河断裂带; F3:安宁河—则木
河断裂带; F4:大凉山断裂带; F5:马边—盐津断裂带; F6:莲
峰—昭通断裂带; F7:小江断裂带; F8:红河断裂带; F9:曲江
断裂带; F10:石屏断裂带; F11:龙蟠—乔后断裂带;
F12:大具断裂带; F13:金沙江断裂带
3 时间—震级可预报统计模型
对于表1中的双震或震群型地震,在本研究中均作为1次能量释放,需要进行相应的预处理。例如1989年4月16日和4月25日四川巴塘两次6.7级地震,以各自能量相加再换算为震级,在后面的计算中视作1989年4月16日6.9级地震。
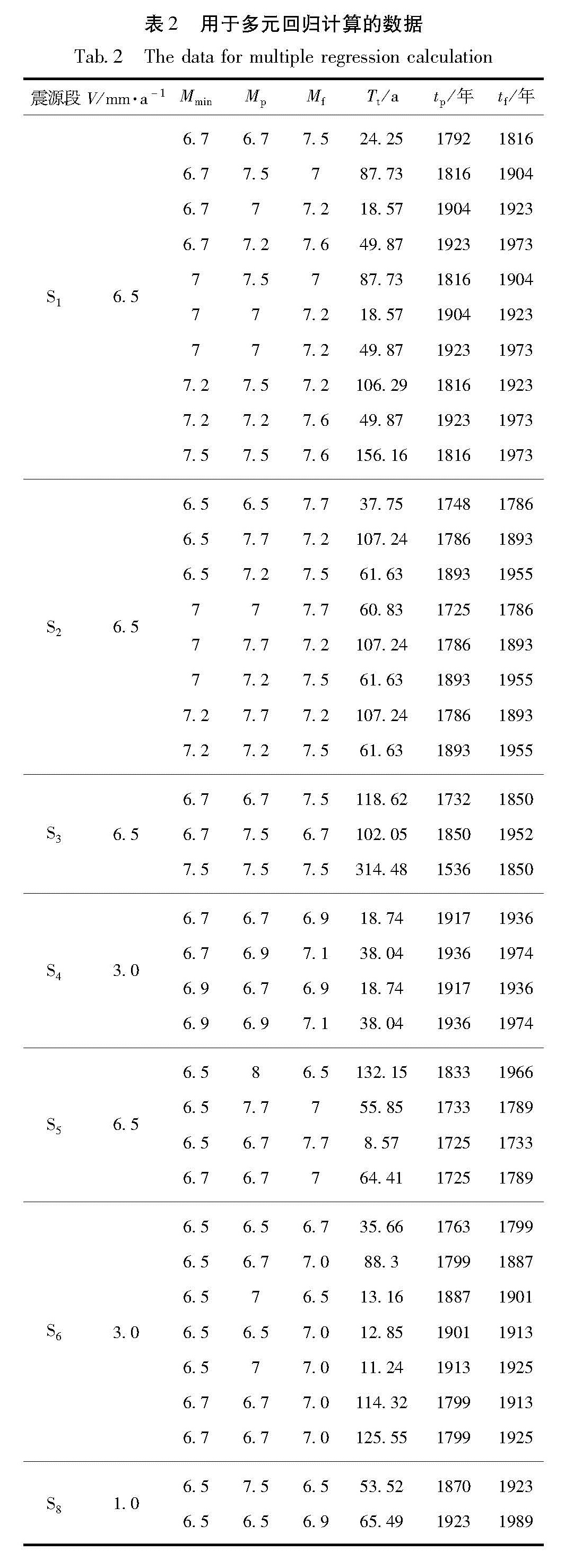
表2是用于多元回归计算的数据。对于每一个震源段,计算不同震级以上相邻地震间的时间间隔Tt、Mp和Mf 。表2中的各震源段的断层滑动速率V,来源于Gkarlaouni等(2008)综合多位研究者的结果得到的川滇地块及邻区的主要断层段的长期滑动速率数据,他取各断层面的宽度均为15 km。
Panagiotopoulos(1995)在计算中美洲和加勒
比海地区的时间—震级可预报统计模型时,在回归计算中去除一些造成残差过大的数据组,以增大多元回归的相关系数; 本研究沿用其处理方法,表2列出了最终参加计算的38组数据。我们得到的川滇地块边界断裂带的回归方程为
lnTt =0.39Mmin+0.37Mp-0.21lnV-3.49,(8)
Mf=0.42Mmin-0.38Mp+0.89lnV+6.37.(9)
式(8)为研究区的时间可预报统计模型,其回归残差标准差和相关系数分别为0.29和0.57。在式(8)中,Tt与Mp之间为正相关,表明上一次地震震级越大,则到下一次地震发生的时间间隔越长; Tt与V之间为负相关,表明断层滑动速率越高,则到下一次地震发生的时间间隔越短。式(9)为研究区的震级可预报统计模型,其回归残差标准差和相关系数分别为0.23和0.74,式中可看出上一次地震震级越大则下一次地震震级越小,断层滑动速率越高则下一次地震震级越大。这2个方程是符合常识的,说明川滇地块边界断裂带的时间—震级可预报统计模型是成立的。
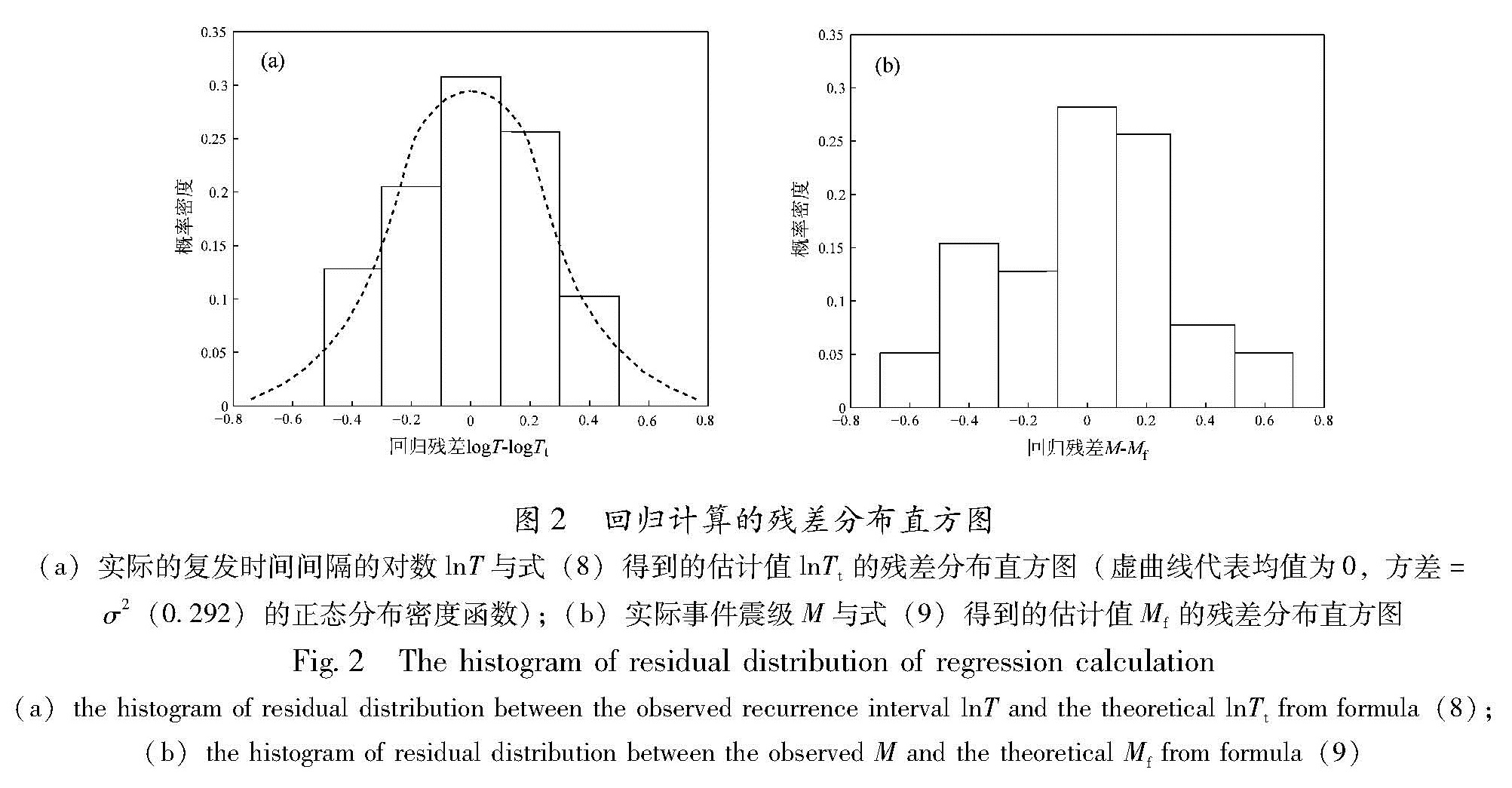
图2a是实际的复发时间间隔的对数lnT与式(8)得到的理论值lnTt之间的残差分布情况,其回归残差分布的离散性较小; 图2b是实际事件震级M与式(9)得到的理论值Mf的残差分布,其离散性相对较大。
图2 回归计算的残差分布直方图
(a)实际的复发时间间隔的对数lnT与式(8)得到的估计值lnTt的残差分布直方图(虚曲线代表均值为0,方差=
σ2(0.292)的正态分布密度函数);(b)实际事件震级M与式(9)得到的估计值Mf的残差分布直方图
Fig.2 The histogram of residual distribution of regression calculation (a)the histogram of residual distribution between the observed recurrence interval lnT and the theoretical lnTt from formula(8); (b)the histogram of residual distribution between the observed M and the theoretical Mf from formula(9)4 时间相依的概率地震危险性
易桂喜和闻学泽(2000)认为,时间可预报统计模型的回归方程所预测的平均复发间隔与实际之间仍然存在不确定性,可以使用“时间相依的危险性”概率分析方法来估计地震的发生概率。
时间相依的危险性是指在特定时段内复发地震的可能性随着上一次地震以来的离逝时间而增加。这种可能性可用概率表示,设某震源自上一次地震以来经过的离逝时间为Te,若已知直到Te时刻地震仍未发生,则在Te至Te+ΔT之间发震的条件概率Pc为
Pc(Te≤T≤Te+ΔT)=(F(Te+ΔT)-F(Te))/(1-F(Te)).(10)
式中,ΔT为预测时段长度,F(Te)和F(Te+ΔT)分别表示从上一次地震以来经过Te或Te+ΔT时间长度时的累积概率,即
F(u)=∫0uf(T)dT.(11)
式中,f(T)是地震复发间隔的概率密度函数。由于式(8)的残差近似服从方差为σ2、均值为0的正态分布,因此,若给定某震源区的最小震级Mmin,i和上次事件的震级Mp,i以及断层段年平均滑动速率V的对数lnVi,则该震源区至下次事件复发间隔的对数lnTi近似服从于正态分布。
对于给定震源区,考虑“内在的”与“数据的”2种不确定性,用于预测的至下次事件复发间隔的概率密度为一条件密度,即
f(lnTi∣Mmin,i; Mp,i; lnVi)
=1/((2π)1/2×σm,i)exp[(-(lnT-μi)2)/(2σ2m,i)].(12)
式中,μi为条件期望,σm,i为预测分布的总不确定性,由“内在的”与“数据的”2种不确定性相叠加:
σ2m,i=σ2+σ2p,i.(13)
在本研究中σ=0.29,反映了复发间隔(对数)的内在不确定性; σp,i为数据不确定性,由下式估算得到:
σp,i=σ[1/n+∑3i=1∑3j=1ρij( X0 i-Xi)(X0 j-Xj)].(14)
式中,n为样本数(等于38),X0i、Xi分别为式(8)中的自变量及相应的平均值,ρij为式(8)系数的逆矩阵ρ的对应元素。
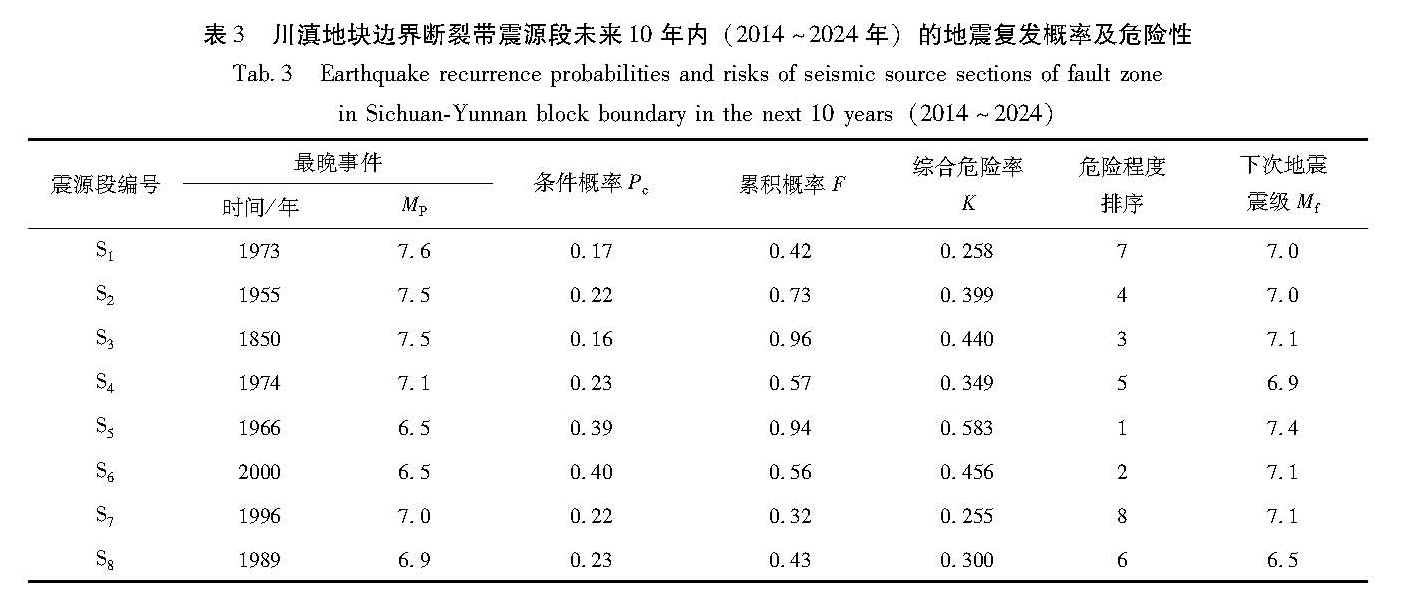
利用上述方法,对8个震源区未来10年(2014~2024年)内地震复发的条件概率Pc及累积概率F进行了估算(表3)。
条件概率Pc指已知上次地震后经过Te时段地震仍未复发,而在给定的未来时段内复发的可能性; 累积概率F反映的是自上次地震以来至关心时刻的累积地震潜势。本研究沿用经验性加权综合危险率K(易桂喜,闻学泽,2000)对各震源区的危险程度进行排序(表3)。
K=0.65Pc + 0.35F.(15)
5 结论
本研究利用断层长期平均滑动速率计算地震矩年变化率,得到了川滇地块边界断裂系统地震复发的时间可预报统计模型及震级可预报统计模型。这2个方程是符合常识的,说明川滇地块边界断裂带的时间—震级可预报统计模型是成立的。
使用时间—震级可预报统计模型对川滇地块边界断裂带的8个震源段未来10年内的时间相依的概率危险性计算结果表明,综合危险率K值最高的3个震源段依次为S5段(小江断裂带)、S6段(红河、曲江、石屏断裂带)、S3段(安宁河—则木河、大凉山断裂带),其中S3、S5段的累积概率F分别达到0.94和0.96,S6段的条件概率Pc为0.40,均高于其它段的值; 计算得到S5、S3、S6段下次地震的震级分别为7.4、7.1、7.1级。在8个震源段中,计算出的下次发生地震的最高震级是7.4级,位于S5段。
在川滇地块边界断裂带的8个震源段中,按照危险程度排序的前3名中的第1、第3名位于南东边界,第2名位于南西边界,表明未来10年内川滇地块南部边界发震的危险性高于北部边界; 预期的下次发生的最高震级地震位于南东边界。
闻学泽研究员为本研究提供了相关的计算程序及构造底图,杜方研究员提出了修改意见,在此一并表示感谢。
- 程佳,刘杰,甘卫军,等.2011.川滇菱形块体东边界各断层段强震演化特征研究[J].中国科学(D辑):地球科学,41(9):1311-1326.
- 皇甫岗,李忠华,秦嘉政,等.2007.川滇菱形块体强震活动关联分析[J].地震研究,30(3):205-209.
- 黄圣睦,朱航.2002.川滇强震活动图像特征与趋势讨论[J].四川地震,(1):16-19.
- 李坪,汪良谋.1975.云南川西地区地震地质基本特征的探讨[J].地质科学,(4):308-325.
- 骆佳骥,崔效锋,胡幸平,等.2012.川滇地区活动块体划分与现代构造应力场分区研究综述[J].地震研究,35(3):309-317.
- 邵辉成,金学申.1999.区域时间和地震级可预报模型在华北及西南地区的应用[J].地震学报,21(3):291-296.
- 闻学泽,杜方,龙锋,等.2011.小江和曲江—石屏两断裂系统的构造动力学与强震序列的关联性[J].中国科学(D辑),41(5):713-724.
- 易桂喜,闻学泽.2000.时间—震级可预报模式在南北地震带分段危险性评估中的应用[J].地震,20(1):71-79.
- 易桂喜.1998.时间—震级可预测模式及其应用研究进展[J].国际地震动态,(11):8-13.
- 张建国,皇甫岗,龙飞.2014.巽他地块的构造演化与介质特性的动力学意义[J].地震研究,37(3):323-331.
- Gkarlaouni Ch.,Papadimitriou E.E.,Karakostas V.G.,等.2008.断层相互作用对中国川滇地区地震危险评估的意义[J].地震学报,30(2):176-197.
- Panagiotopoulos D.G..1995.Long-Term Earthquake Prediction in Central America and Caribbean Sea Based on the Time-and Magnitude-Predictable Model[J].BSSA,85(4):1190-1201.
- Papadimitriou E.E..1993.Long-term Earthquake Prediction along the Western Coast of South and Central America Based on a Time Predictable Model[J].Pure Appl.Geophys,140(2):301-3l6.
- Papazachos B.C.,Karakaisis G.F.,Papadimitriou E.E.,et al..1997.The Regional Time-and Magnitude Predictable Model and its Application to the Alpine-Himalayan Belt[J].Tectonophysics,(271):295-323.
- Papazachos B.C.,Papadimitriou E.E..1994.An Application of the Time-and Magnitude-predictable Model for the Long-term Prediction of Strong Shallow Earthquakes in the Japan Area[J].BSSA,84(2):426-437.
- Papazachos B.C.,Papaioannou C.A..1993.Long-term Earthquake Prediction in the Aegean Area Based on a Time-and Magnitude Predictable Mode1[J].Pure Appl.Geophys,140(4):593-612.
- Papazachos B.C..1989.A Time-predictable Model for Earthquake Generation in Greece[J].BSSA,79(1):77-84.
- Papazachos B.C..1992.A Time and Magnitude PredictableModel for Generation of Shallow Earthquakes in the Aegean Area[J].Pure Appl.Geophys,138(2):287-308.
- Paudyal H.,Shanker D.,Singh H.N.,et al..2009.Application of Time-and Magnitude-predictable Model in the Central Himalaya and Vicinity for Estimation of Seismic Hazard[J].Acta Geodaetica et Geophysica Hungarica,44(2):213-226.
- Yadav R.B.S.,Shanker D.,Chopra S.,et al..2010.An Application of Regional Time and Magnitude Predictable Model for Long-term Earthquake Prediction in the Vicinity of October 8,2005 Kashmir Himalaya Earthquake[J].Natural Hazards,54(3):985-1014.