基金项目:中国地震局地震科技星火基金青年项目(XH14067Y)、中国地震局地震研究所所长基金(IS201266113)和中国地震局震情跟踪专项工作任务(2014020212)联合资助.
(First Crust Monitoring and Application Center,CEA,Tianjin 300180,China)
seismic ground acceleration time history; evaluation method of the consistence; tectonic information; Tianjin earthquake; Tangshan area
备注
基金项目:中国地震局地震科技星火基金青年项目(XH14067Y)、中国地震局地震研究所所长基金(IS201266113)和中国地震局震情跟踪专项工作任务(2014020212)联合资助.
为评价使用各种方法获得地震动加速度时程与区域内地震动加速度时程观测资料的一致性,提出一种能够综合时频特性的地震动时程一致性评价指标及其相对性判据,该方法可以量化分析待评价地震动时程对区域构造信息的反映能力。通过评价唐山地区陡河地震台和四座楼地震台模拟结果与实际观测结果的一致性,给出了实用化的算例。
To evaluate the consistence of the seismic ground acceleration time history between by use of different method and regional observation,we put forward a kind of assessment index of the consistence of the seismic ground time history which could synthesize the time-frequency characteristics and its relative consistency criterion. This method could quantitatively analyze the reflection ability of evaluated seismic ground time history on the regional tectonic information. We compared the simulation result with the realistic observation result of Tangshan M4.7 earthquake in 2012 recorded by Douhe Station and Sizuoluo Station in Tangshan area,and gave a practical example.
引言
各类超限建筑和大跨结构的抗震设计要求提供具有能够反映区域构造信息的加速度时程作为地震动输入以满足结构时程分析的需要。但是现有强震观测成果具有空间分布不均匀性、不可重现性以及场地条件依赖性的特点,因此在与工程场地环境完全一致的强震观测波形缺失的情况下,时程分析多采用场地条件相似地区的天然波形或人工合成波作为输入。然而,不管是天然波的选择,还是人工地震动的合成均横跨地球科学与工程科学两大研究领域,涉及到震源模式、地震波传播方式、传播介质影响、场地条件约束、地震动基本参数标定、地震动的模型简化以及地震动的工程预测等诸多环节,其中每一项都错综复杂且饱含不确定因素(张翠然,陈厚群,2008)。因此,所选择或者合成的地震动加速度时程在应用于工程实际之前,必须考虑该地震动时程能否代表工程厂址周围的地震环境特征和场地条件特征。
人工合成的地震动时程需要达到什么样的程度才能代表以上地震环境和场地条件,国内工程场地地震安全性评价工作中人工地震动合成主要通过不同周期点上反映区域地震危险性的目标谱5%范围内的控制精度来对合成波质量进行评价(胡聿贤,1999)。这种方法主要使用某种绝对指标,如地震动绝对加速度反应谱、某实测地震动时程作为目标,以合成波或者所选择的天然波与目标之间的逼近程度作为地震动反映特定环境能力的评价指标(Anderson,2004; 孟庆筱等,2012)。但是值得思考的是,地震事件发生过程中获得的强地面运动加速度时程往往由于震源特性、传播路径以及场地条件的原因而具有很大的差异性,即使是相同地震台站所观测得到的两个水平地震动分量之间都会由于破裂的方向性效应和传播介质的各向异性等因素而产生不同。因此,在地震动时程之间差异性普遍存在的情况下,使用上述单一且具有绝对性的指标进行评价难免有失偏颇,亟需提出一种综合性评价指标和建立在区域地震动统计特性之上的相对性判据来反映地震动输入的区域构造信息反应能力。
本文综合考虑地震动在幅值、频谱和持时三要素的各类特征值,构建总体一致度指标SZ来表示代表地震动时程两两之间的绝对相似程度; 然后基于研究区内现有的地震动观测资料中相同台站的两个水平地震动加速度分量之间的绝对相似程度的统计特性来给出一种表征区域构造信息相对性判据; 最后利用2012年5月28日唐山M4.7地震事件的地震动模拟结果(孟庆筱等,2014a,b),使用2000年以来国家测震台网37个台站观测得到的5个M≥3.0地震事件的数据得到了唐山地区地震动时程的一致度评价判据标准,并用近断层陡河地震台(DOH)和远场四座楼地震台(SZL)模拟结果作为算例对本文和标准判据进行了检验,证实了该方法的可行性和实用性。值得注意的是,本文重点强调方法构建,因此可能在算例数据的充足程度方面有所欠缺。
1 区域构造信息反映能力综合评价指标构建
2 判据构建方法和应用算例
在本文的以上部分,我们构建了一个待评价地震动加速度时程与目标地震动加速度时程之间的构造信息反映能力的综合评价指标。需要明确的是,不管是通过相似地区天然地震动选波、工程学方法还是地震学方法获得的地震动加速度时程最终都会给出一组波进行备选,因此面临评价这些备选波或者待评价波的区域构造信息反映能力的问题。然而上文给出的综合评价指标只能给出一对加速度时程之间的一致性程度,但是一致性程度指标达到什么范围才算是可以充分反映区域构造信息,或者说一致性程度指标达到什么范围强地面运动模拟结果效果良好,解决这些问题有必要给出相对性判据的构建方法。
2.1 目标地震波组总体一致度判据构建方法地震事件中相同台站观测到的两个水平方向分量的一致性是良好的,我们将研究区内所有地震事件过程中的所有相同台站观测得到的加速度时程水平方向内两个分量的集合称之为研究区内的目标地震动组,其中共计N对地震动加速度时程。通过计算目标地震动组中各个地震动对的总体一致度SZ,则可以求得该研究区内SZ的取值区间[SZmin,SZmax]。 假设存在一条待评价加速度时程a(t)与目标地震动组中的第i条目标地震动加速度时程Acci(t)的总体一致度SZi属于[SZmin,SZmax], 则a(t)与Acci(t)之间的一致性要比目标地震动组中至少1个台站的水平面内地震动加速度时程的两分量之间的一致性要高, 此时我们认为a(t)可以充分反映该区域内的构造信息。为了进一步获得量化的相对判据,我们建议给出如下的目标地震动组中所有地震动对总体一致度SZ的累积概率分布曲线,有
F(x)=P(SZ≤x).(6)
其中, F(x)为累计概率分布函数,即随机变量SZ小于或者等于某个数值x的概率。
2.2 2012年唐山M4.7地震算例2012年5月唐山发生M4.7地震,孟庆筱等(2014a,b)使用基于有限单元法的非连续数值模拟给出了该地震事件过程中的强地面运动结果。这对本文所提出的地震动加速度时程区域构造信息反映能力评价方法的应用提供了一次宝贵的机会。为了进行目标地震波组总体一致度判据的构建,我们获得了该区域内2000年1月至今的M≥3.0地震动观测资料,包含5次M≥3.0地震事件,其地震目录及其简单情况如表4所示。其中国家测震台网在研究区域内共有37个测震台站(郑秀芬等,2009),台站分布见图1。将以上实际观测得到的地震动加速度时程作为目标地震动组,将孟庆筱等(2014b)所得到的陡河地震台(DOH)和四座楼地震台(SZL)的数值模拟结果作为待评价地震动。需要注意的是,本文重点考虑一致度的评价方法且只使用了唐山地区5次地震事件过程中的37个测震台站的数据,因此以下判据不宜直接推广,但可以作为今后提出判据的一个参考范例。
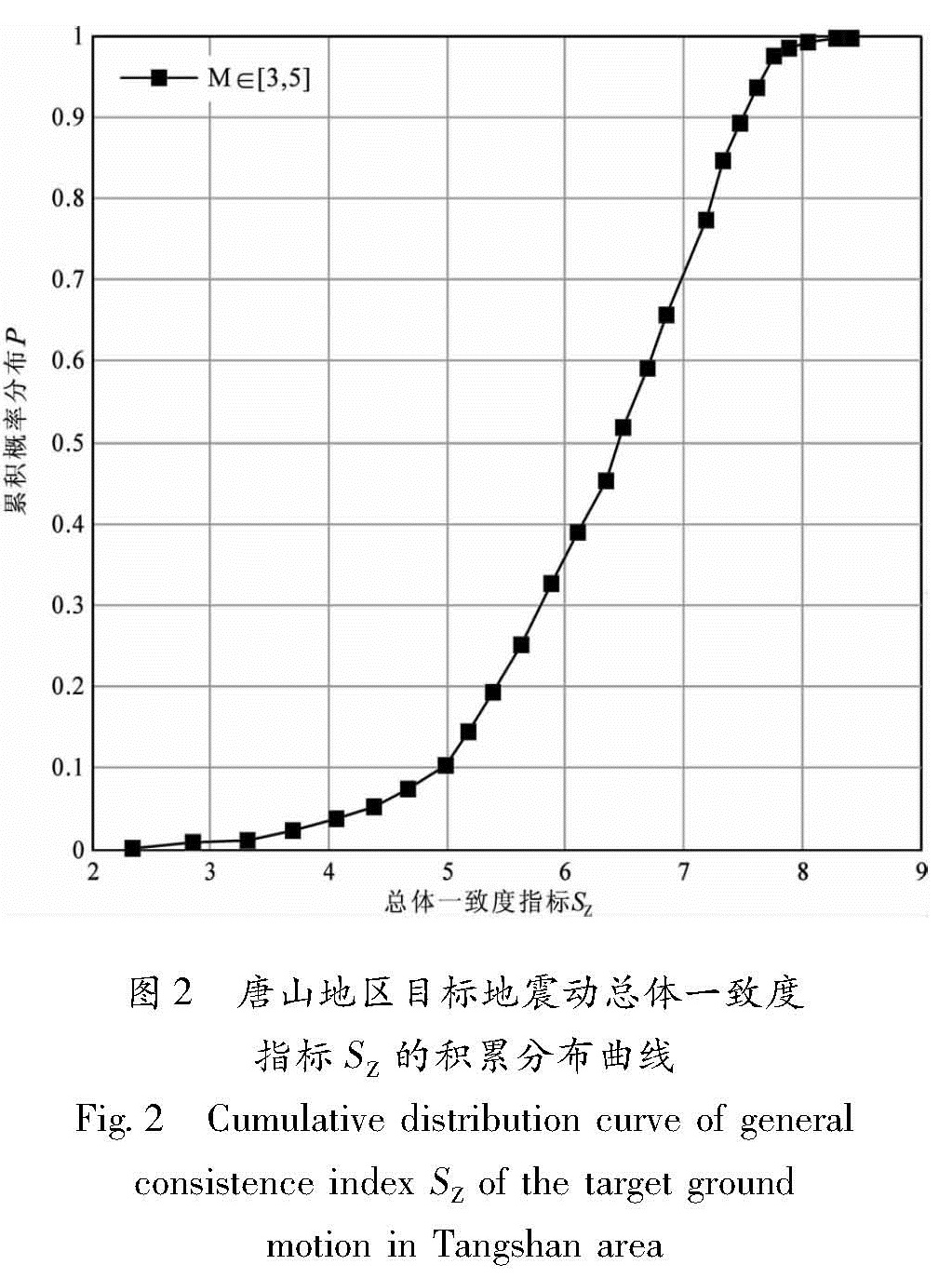
图2为4.7级地震情况下地震动时程对总体一致度SZ的累积概率分布,由图2可见:该情况下,总体一致度指标SZ的取值区间为[2.1,8.4],说明该区域内相同台站观测得到的地震动时程的两个水平分量的之间差异性分布较为分散。于此同时,我们获得了研究区内构造信息反映能力的判据,即当待评价地震动与目标地震动的总体一致性指标SZ介于[2.1,8.4]区间内时,我们认为待评价地震动初步具备反映构造信息的能力,模拟结果较好,可以满足构成工程结构地震动输入对区域构造信息的要求。图1 唐山地区测震台站和2000年1月以来研究区M≥3.0地震震中分布示意图
Fig.1 Seismic station and epicenter distribution of M≥3.0 earthquakes in Tangshan area since Jan., 2000根据孟庆筱等(2014b)对2012年唐山M4.7地震陡河台(DOH)和四座楼(SZL)水平面内东西分量的模拟结果和该地震事件中相应台站的观测结果,计算得到2组地震动对的总体一致度指标SZDOH=7.23,SZSZL=2.07。说明孟庆筱等(2014a,b)对陡河地震台的模拟结果与四座楼地震台模拟结果相比具有更好的效果,或者说对于该地区的构造信息具有更为充分的反映能力。同时,如图3可见,SZSZL=2.07明显小于2.1,不属于[2.1,8.4]区间,其积累概率为0,说明四座楼地震台的模拟结果未能达到现有观测资料中相同台站相同地震事件中两个水平地震动分量之间的一致度,因为本文认为四座楼地震台的模拟结果较差,缺乏对区域构造信息的反映能力,是一个较为失败的强地面运动模拟结果; 同时陡河地震台的模拟结果则明显较好,其积累概率为0.87,说明该模拟结果与87%的观测结果相比一致性更好。图2 唐山地区目标地震动总体一致度指标SZ的积累分布曲线
Fig.2 Cumulative distribution curve of general consistence index SZ of the target ground motion in Tangshan area3 结论
本文通过分项地震动参数一致度Ci构建了能够考虑地震动时程时频特性的总体一致度指标SZ,同时给出了判据的构建方法。使用唐山地区2000年1月以来观测得到的M≥3.0的5次地震事件观测波形给出了唐山地区小震情况下的区域构造信息反映能力判据。在此基础之上,使用孟庆筱等(2014a)的二维有限元方法模拟得到的陡河地震台(DOH)和四座楼地震台(SZL)的模拟结果作为待评价地震动时程给出了实用化的范例,并对结论进行了简要分析,检验并证明了区域构造信息反映能力指标体系构建方法的有效性。
唐山地区5次地震事件的观测波形数据由中国地震局地球物理研究所“国家数字测震台网数据备份中心”提供,在此表示感谢。同时感谢郑秀芬研究员对本文的悉心指导以及宝贵意见。
地震动参数往往具备幅值、频谱和持时三大主要特性。我们将拟作为工程结构地震动输入的地震动加速度时程或者强地面运动模拟过程中所获得的某一条加速度时程结果,称为待评价加速度时程; 同时将研究区域内实际地震过程中观测得到某一条波形,称为目标加速度时程。目标加速度时程是研究区域内实际得到的地震动观测结果,因此包含了震源特性、传播路径和场地效应的影响,本文拟通过待评价加速度时程与目标地震动的一致性比较,提出区域构造信息反映能力的综合评价指标,即待评价地震动加速度时程与目标地震动加速度时程一致性越好,则待评价地震动加速度包含了越多的构造信息。其具体步骤为:首先选择可以有效表征地震动特性的各类地震动参数并计算待评价加速度时程与目标加速度时程之间各地震动参数的分项一致度Ci,然后构建地震动参数的总体一致度SZ来表征以上两条地震动时程之间的总体一致程度。最后,我们会进一步说明该指标的实际使用方法,并给出算例。
1.1 地震动参数分项一致度Ci1.1.1 地震动参数的选取工程上所关心的强地面运动是由震源释放出来的地震波引起的(近地表)地面运动,是由不同频率、不同幅值在一个有限时间范围内组成的集合。而地震动加速度时程作为一个不规则的时间函数,使用各种数学和力学处理方法可以获得一系列表示地震动特性的特征值,大致可以分为幅值、频谱和持时三类。前人对地震动反映地震环境的能力评价中,大多数使用较为单一的绝对指标,往往选择以上各类指标中的一个或者几个,难以全面的反映两个地震动时程之间的综合一致程度。因此,本文选择Arias持时、能量持时、Arias烈度、能量积分、峰值加速度、峰值速度、峰值位移、反应谱、傅里叶谱共计9个地震动参数来综合表示地震动特性,其具体表达式如表1所示。
对于所有的地震动参数比较而言,考虑2条地震动加速度时程a1(t)和a2(t)。令vi(t)和di(t)代表该地震动的速度时程和位移时程。令SA(fi)为5%阻尼比情况下fi时的加速度反应谱,令FSi(fi)为第i条地震动时程在频率fi时的傅里叶谱值。Arias积分为
IAi(t)=(π)/(2g)∫t0a2i(τ)dτ.(1)
Arias(1970)将Arias 烈度定义为IA=IA(Td),其中Td为加速度时程的完全持时。地面运动的能量与速度积分相关,而不是加速度积分相关,因此,我们将能量积分定义为
IEi(t)=∫t0v2i(τ)dτ.(2)
地震动携带的全部能量与IE(Td)成线性相关,完整的关系式包含了波速和地面介质密度。
注: ai(t)、 vi(t)和di(t)为第i条地震动时程的相关速度和位移,其中0≤t≤Td,Td为地震动的总持时.1.1.2 分项一致度Ci计算方法为了评价特征地震动时程反映实际工程地震环境和场地条件的能力,必须建立待评价的特征地震动时程与代表地震环境和场地条件的目标地震动波组之间的一致程度的标准,即地震动参数分项一致度Ci。
(1)首先定义一般化的单值参数的一致度指标S,对于单值地震动参数对(p1,p2)而言,两者的一致程度为S(p1,p2),有
S(p1,p2)=10exp{-[((p1-p2))/(min(p1,p2))]2}.(3)
下面以地震动峰值加速度(PGA)为例进行说明:地震动峰值加速度Spga(C5)用来表示不同地震动时程地震动峰值加速度之间一致程度。 令Ai=max〖JB<1|〗ai(t)〖JB>1|〗, 则定义Spga=S(A1,A2)。
使用该指标具有3个方面优势:(1)当参数之间的差异性增大时,该指数将会单调递减,因此该指标可以用于遗传算法等优化类算法通过寻找最大相似度来获得最优指标;(2)该指标是对称的,因此不论是加速度a1(t)和a2(t)哪个的PGA更大,该指标都会给出相同的参考结果;(3)小的差异性不会导致该指标迅速下降,当差异仅仅为参数本身的0.5倍时,该指标的评价值约为8,当指标大于2~3时,在工程应用意义上认为是不合适的。
(2)定义频域内的函数类地震动参数的一致度指标S。对于各种频谱类地震动参数,其表达形式一般为频域内的各种形式的函数。但是通常的观测波和人工合成地震动并不能覆盖整个频域。观测值往往受限于仪器响应和噪声水平,而人工地震动往往取决于其生成方法。因此必须考虑不同频带上的不同一致程度。因此本文将整个频域划分为表2中B1~B9 9个频带,同时令B10介于0.05~50.0 Hz以代表整个频域。根据地震动各个频段的重要性不同,我们设定各个频带的间距基本上在对数坐标下线性增长,有
S=∑10i=1ki×10exp{-[((p1(fi)-p2(fi)))/(min(p1(fi),p2(fi)))]2}.(4)
其中,ki为频带权重系数,p(fi)为第i个频带上的相应地震动参数。
进一步的实际应用中,可以根据地震环境和场地条件,调整相应的频带权重。例如,当厂址所在区域范围内存在远场大震或者深软场地,且建筑结构形式对长周期分量反应明显时,可以适当增加长周期频带的权重,从而达到重点考虑长周期分量的效果。在本文中,我们暂时不考虑ki的影响,在表3中将S统一取做各个频带的平均值。因此,我们使用上述两种分项一致度Ci的计算方法,得到拟选用的地震动参数的分项一致度指标C1~C9,如表3所示。
注: ai(t)、 vi(t)和di(t)为第i条地震动时程的相关速度和位移, 其中0≤t≤Td, Td为地震动的总持时.表3 一致度分项指标Ci
Tab.3 Subentry indexes of the consistence Ci1.2 总体一致度SZ我们已综合考虑了地震动在幅值、频谱和持时三要素中的不同参数的分项一致系数。但是单一化的分项一致系数难以有效体现地震动时程对的综合一致程度,因此有必要构建总体一致度SZ。对于需要进行一致度评价的2条地震动加速度时程a1(t)和a2(t)而言,我们选取并构造了C1~C9共计9个一致度指标,令这9个指标的算术平均值作为总体一致度指标,有
SZ=∑10i=1Ci.(5)
其中,SZ为总体一致度指标; Ci为特征值一致度指标(表3)。
在时域方面,峰值速度PGV、峰值位移PGD、Aria烈度和能量积分在指标构建过程中使用了相同的表达式。Arias烈度和能量积分指标可用来评价地震动持时特征,因此我们提出使用C1和C2两个指标来灵敏的评价地震动时程标准化之后的积分特征差异性,如表3所示。
在频域方面,C8和C9是两个频域指标,分别考虑5%阻尼比情况下的反应谱和傅里叶谱。虽然两者在某些程度上具有一定的相似性,但是在概念上却完全不同。反应谱在高频和低频段上具有渐近线性质,但是傅里叶却没有,同时反应谱更为平滑。因此,有必要同时使用以上两个频域指标。本文使用地震动时程不同频段内分量计算得到的反应谱和傅里叶谱对地震动频域相似性进行评价。具体来讲,本文使用不同频段内分量评价值的均值作为反应谱和傅里叶谱形状的总体评价值。由于地震动时程的重新构建需要每一个频率点上的傅里叶谱值都正确,因此使用C9指标一一对其标定。
- 虢顺民,李义志.1977.唐山地震区域构造背景和发展模式的讨论[J].地质科学,4(10):305-321.
- 胡聿贤.1999.地震安全性评价技术教程[M].北京:地震出版社.
- 孟庆筱,王太松,韩勇,等.2014a.二维有限元基岩水平向地震动模拟方法及检验[J].大地测量与地球动力学,34(4):9-16,20.
- 孟庆筱,王太松,吕健,等.2014b.唐山断裂带三维构造应力场的数值模拟[J].大地测量与地球动力学,34(1):38-42.
- 孟庆筱,姚运生,胡国新,等.2012.巴东黄土坡滑坡稳定性分析[J].大地测量与地球动力学,32(6):65-70.
- 张翠然,陈厚群.2008.工程地震动模拟研究综述[J].世界地震工程,24(6):150-157.
- 郑秀芬,欧阳飚,张东宁,等.2009.“国家数字测震台网数据备份中心”技术系统建设及其对汶川大地震研究的数据支撑[J].地球物理学报,52(5):1412-1417.
- Anderson J.G..2004.Quantitative Measure of the Goodness-of-fit of Synthetic Seismograms[C].13th World Conference on Earthquake Engineering:1-6.
- Arias A..1970.A Measure of Earthquake Intensity[C]//Hansen R.J. Seismic Design for Nuclear Power Plants.Cambridge,MA:Massachussetle.Institute of Technology Press,438-483.