2.1 有限元分析模型
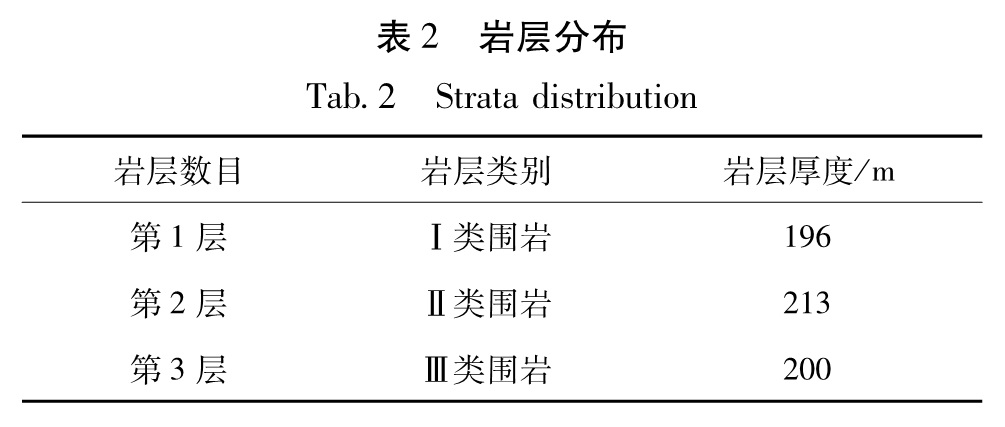
建立三维有限元模型,模型尺寸为Y向610 m,X向660 m,Z向300 m; 岩层和巷道物理力学性能如表1,岩层分布如表2。巷道为半拱形巷道,拱直径4 m,巷道的纵向长度为200 m,衬砌厚度为400 mm。围岩和巷道衬砌使用solid164体单元,人工边界采用无反射边界。岩层材料
Tab.1 The rock mechanics parameter
Tab.2 Strata distribution
采用理想弹塑性DP材料,巷道结构采用C50混凝土,LS-DYNA中通过*MAT_072R3材料模型实现巷道损伤本构。
2.2 地震波的选取与调整
Fig.1 The finite element model of rock(a)
and roadway(b)
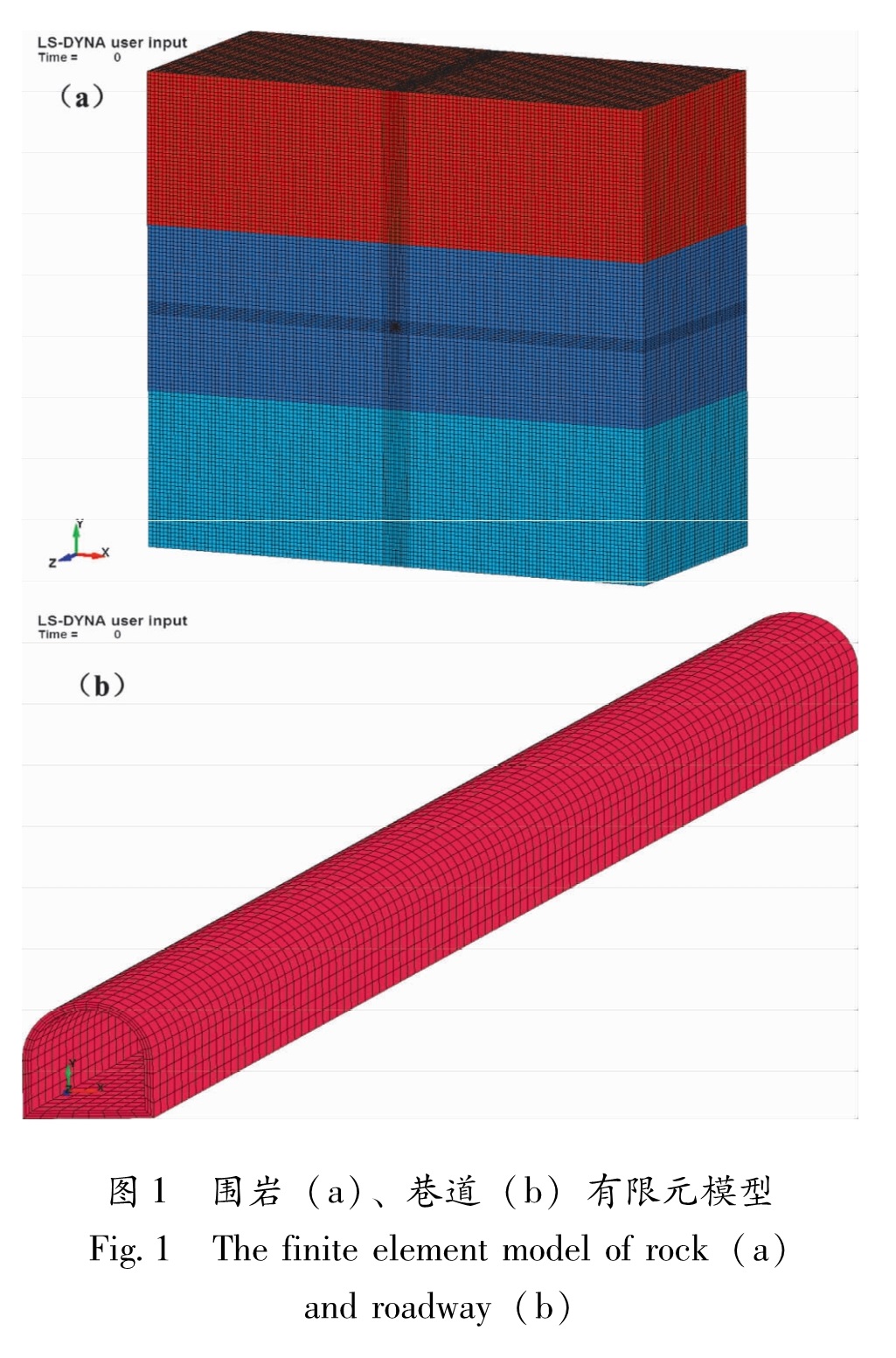
Fig.2 El Centro earthquake wave(NS direction)
度、频谱特性、波的持时的要求,不同地震波参数得出的地震响应可能相差明显,因而选择合理的地震波参数进行动力分析是必要的。本文选用了15 s的El Centro地震波,最大加速度调整为150 cm/s2,如图2所示,地震波在基岩底部沿X水平输入。
2.3 数值模拟结果分析
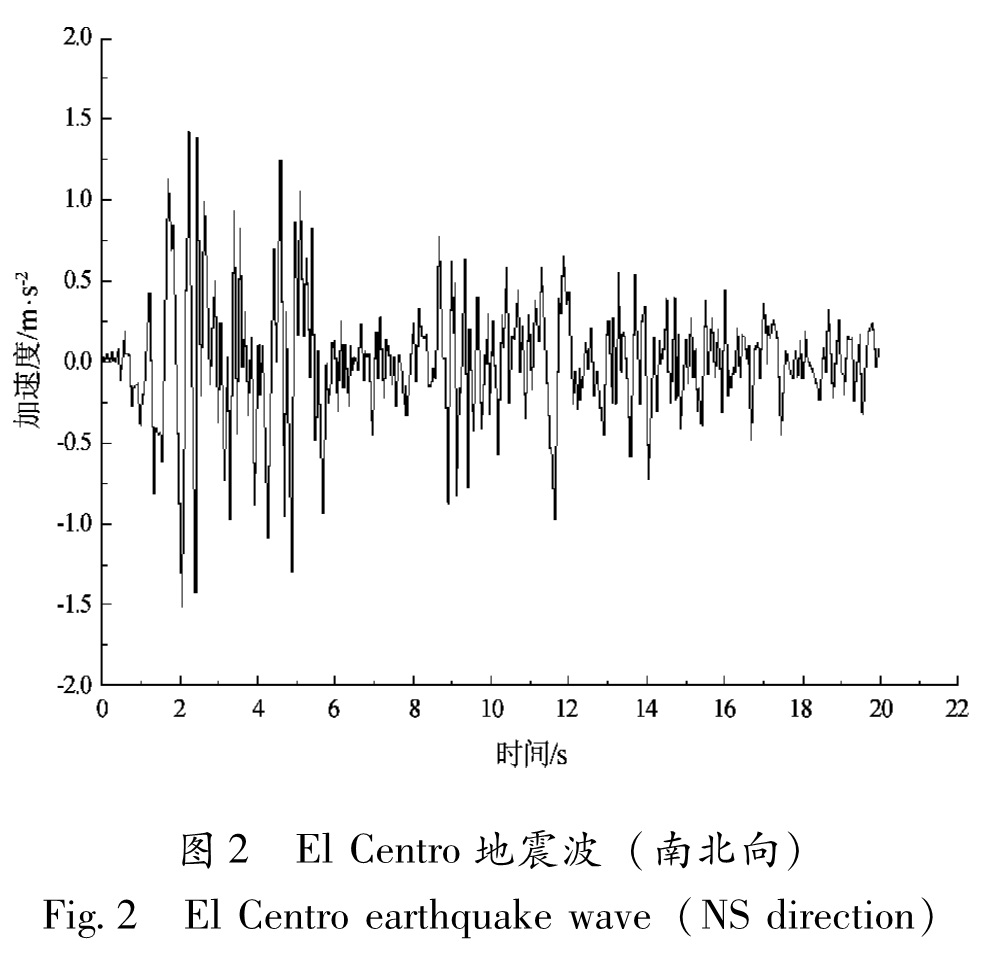
在巷道100 m处截取截面,并在截面不同部位设置观测点,如图3所示。
Fig.3 Observation position of the roadway
2.3.1 巷道应力分析
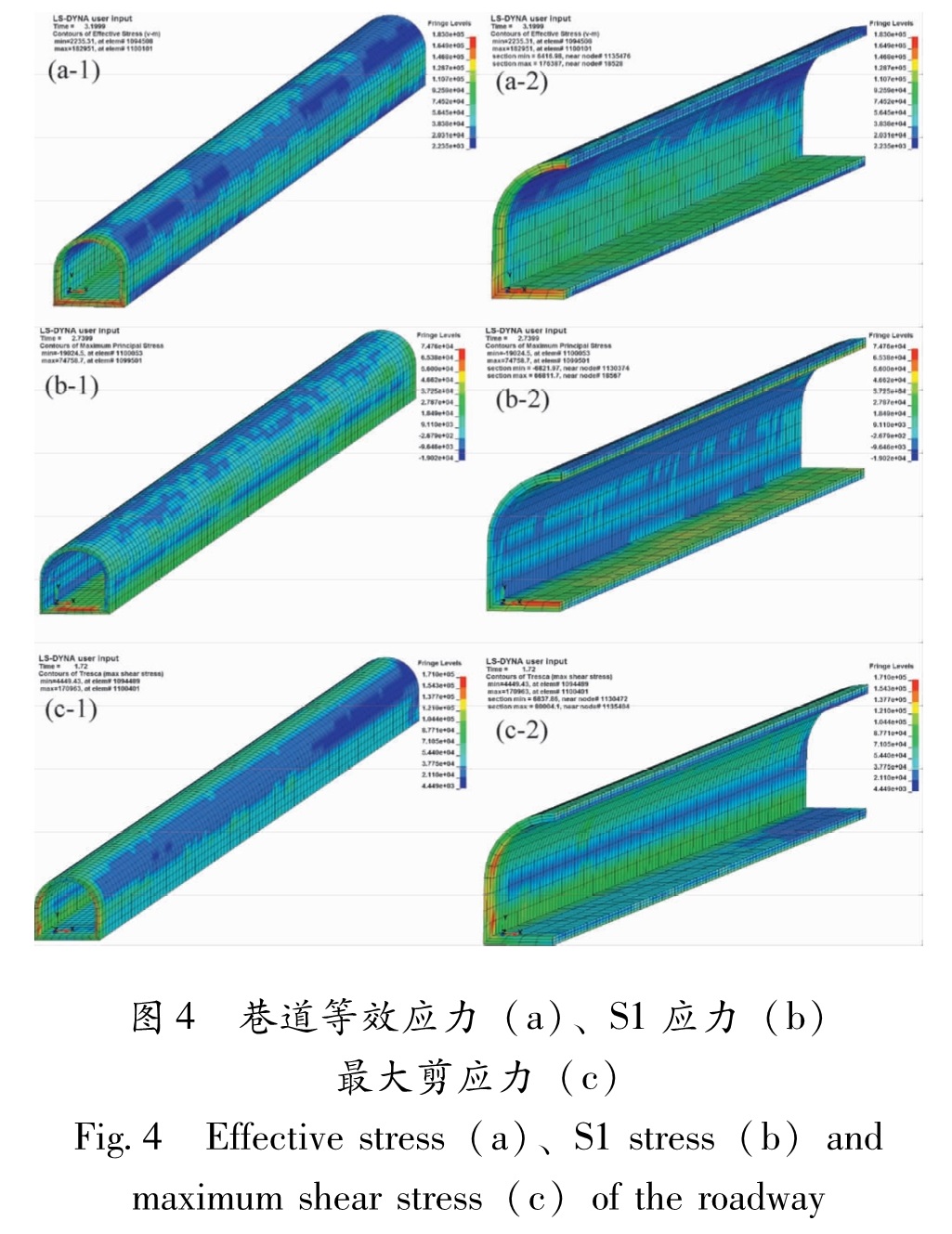
图4为巷道应力的典型分布图,从图中可知,巷道的等效应力和S1主要分布在墙角和拱帮偏下,S3主要分布两侧拱腰处; 最大剪应力在墙角处最大,拱帮偏下处次之; 这说明巷道的墙角立板和拱腰处成了高应力集中区。
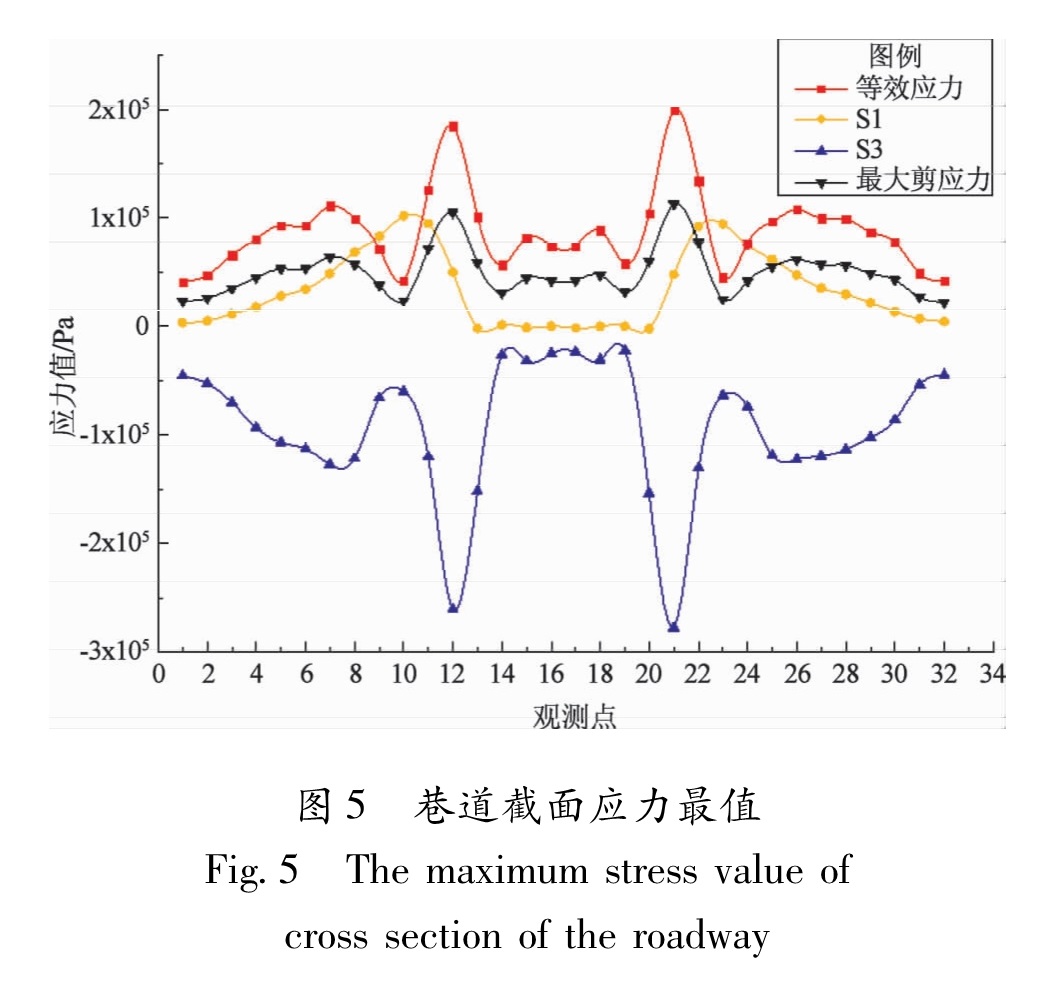
图5为巷道取100 m纵深截面时不同部位的最大应力(等效、S1、S3、剪应力),由图可知,等效应力、S3和最大剪应力的峰值在左右拱帮偏下的位置(5、6、7、26、27、28号点)和墙角立板的位置(12、13、20、21号点); S1峰值在左右拱帮偏下(8号点)和左右立板腰部(10、11、22、23号点)位置; 这说明巷道的拱帮偏下和墙角是拉、剪复合最大应力区,巷道的立板腰部主要受拉应力作用; 地震作用下的高应力反复的加、卸载会对巷道的这些部位造成较大破坏,对于在拉、剪复合应力区的拱帮和墙角破坏更明显,墙角处尤其明显。
最大剪应力(c)
Fig.4 Effective stress(a)、S1 stress(b)and
maximum shear stress(c)of the roadway
Fig.5 The maximum stress value of
cross section of the roadway
2.3.2 损伤分析
图6为巷道的塑性体积应变,从图中可知巷道拱帮发生了明显的塑性体积应变,且由巷道中部向巷道两端扩展时,巷道的塑性体积应变有减小的趋势,但是在巷道的两个端部又有所增大,造成巷道两端塑性体积应变有所增大的主要原因是端部边界条件不同; 其次在巷道内侧的墙角处也出现了明显的塑性体积应变,在巷道发生塑性体积应变的部位(巷道帮部、腰部至墙角立板)积累了明显的损伤,这些损伤使得巷道在这些部位更容易遭到破坏。
Fig.6 Plastic volume strain of the roadway
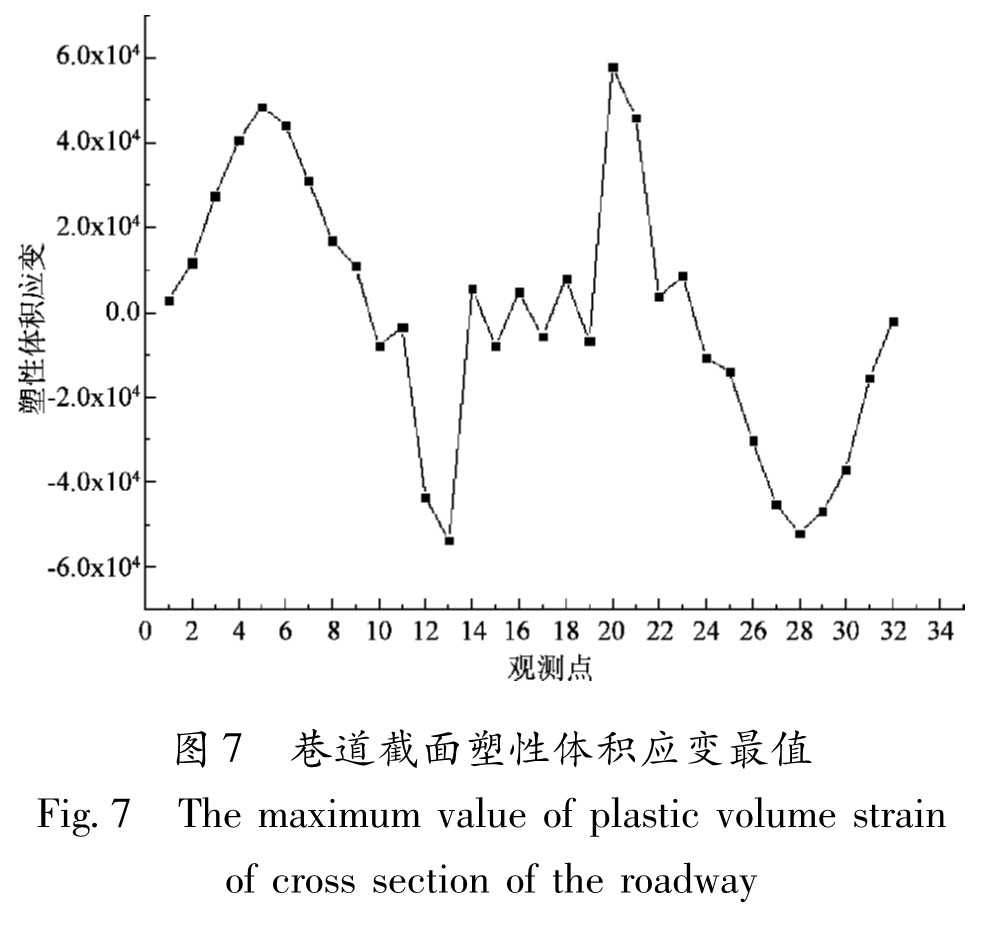
图7为巷道取100 m纵深截面时不同部位的最大塑性体积应变,由图可知,巷道的左右帮部(5、28号点)和墙角底板(13、20号点)的塑性体积应变最为明显,这说明巷道的左右帮部和墙角底板会发生相对于其他部位更明显的变形,这可能造成帮部开裂、墙角底板翘起,同时伴随着小块石飞溅。由于巷道的墙角立板(13、21号点)和帮部偏上(5、28号点)的塑性变形较为明显,因此在这两处积累损伤较为明显,其中墙角底板损伤尤为严重,这说明在地震作用过程中,墙角立板在拉、剪应力反复作用下会积累大量的损伤,拱帮偏上损伤程度也要明显大于其他部位,这会造成墙角立板和拱帮偏上处最先发生破坏,随着这种破坏的扩展,就可能引发立板和上帮失效,进而引发整个巷道的破坏。
Fig.7 The maximum value of plastic volume strain
of cross section of the roadway
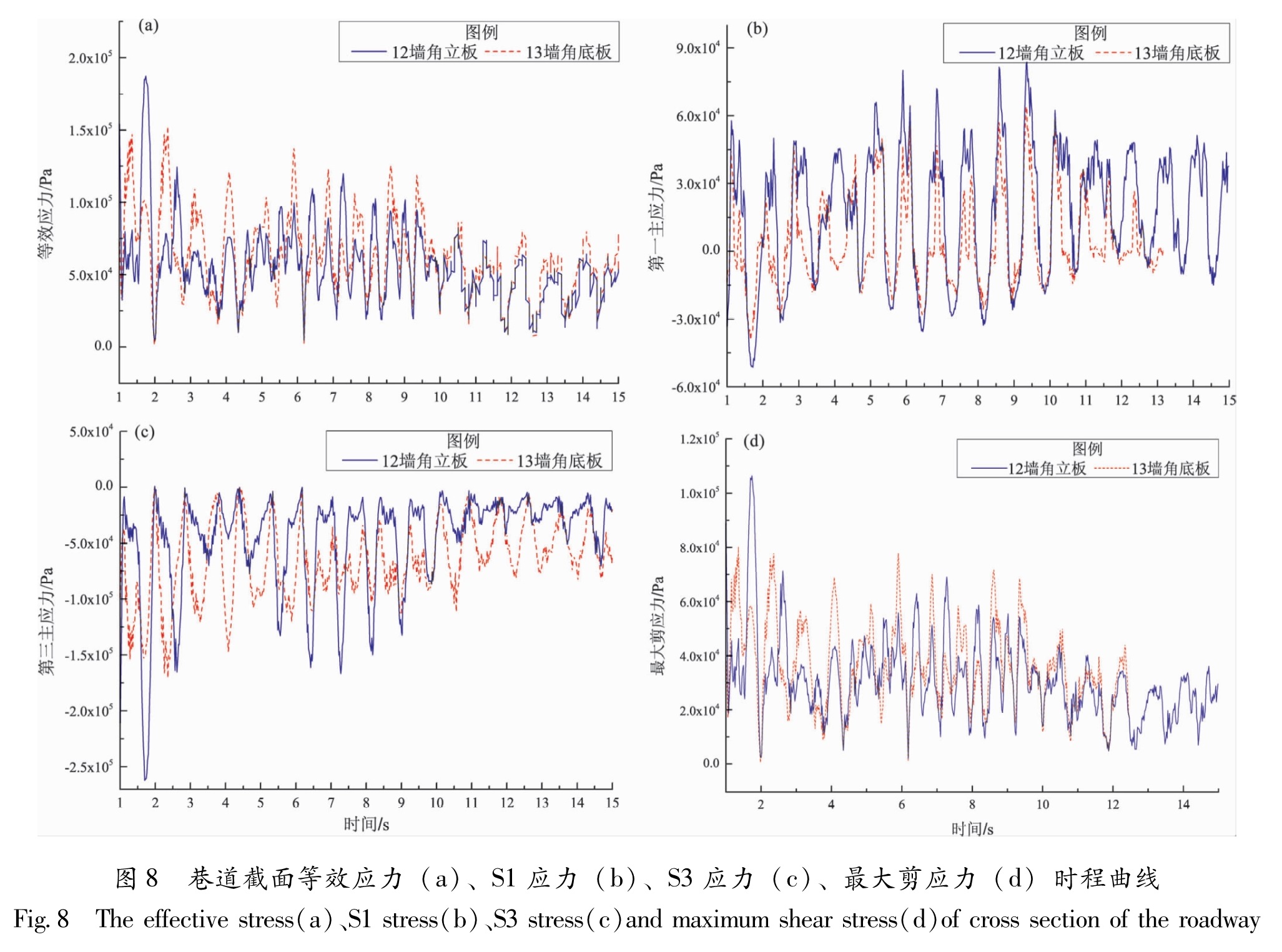
图8 巷道截面等效应力(a)、S1应力(b)、S3应力(c)、最大剪应力(d)时程曲线
Fig.8 The effective stress(a)、S1 stress(b)、S3 stress(c)and maximum shear stress(d)of cross section of the roadway
2.3.3 时程分析
由上述可知,地震作用过程中巷道的墙角处应力最为复杂,变形最为明显。本节提取了巷道墙角12和13号观测单元的应力和塑性体积应变的时程曲线。分析图8的巷道墙角立板和底板的应力时程曲线可知:巷道墙角的应力在t=2 s和t=8 s会出现两个峰值,在基道取100 m纵深截面的前提下,t=2 s时的应力峰值与输入加速度的峰值时刻基本一致,t=8 s的应力峰值较加速度峰值有所提前; 巷道墙角立板的等效应力在整个时程中小于墙角底板的等效应力,S1应力的墙角立板的应力大于底板的应力,S3应力中间时刻较为明显,最大剪应力墙角底板在整个过程中基本大于立板。
图9为巷道墙角的塑性体积应变时程曲线。由时程曲线可知立板和底板的塑性体积应变变化基本一致,底板的塑性体积应变大于立板的,从而使得底板的损伤大于立板。故可得出在整个地震过程中,半拱形巷道的墙角底板应作为抗震的重点防护部位。
Fig.9 Plastic volumetric strain time history curve
of cross section of the roadway