使用现代统计物理的理论和方法来研究地震预测问题,已成为物理学与地震学之间最为活跃的一个交叉领域(吴忠良,陈运泰,2002)。

美国加州大学Rundle等(2000b)利用图像信息学(Pattern Informatics,简称PI)算法,对加州地震活动性进行分析(Rundlle et al,2000a,b; Tiampo et al,2002a)。PI算法着眼于地震活动的“增强”与“平静”特点,去除背景地震活动,从而检测地震发生高概率区域(即地震热点)。国内外学者均进行过强震危险性预测的回溯性检验和中长期地震预测,如针对于全球M≥7.0强震(Holliday et al,2005a,b)、日本中部(Nanjo et al,2005)、中国台湾(Chen et al,2005)、川滇地区(蒋长胜,吴忠良,2008)、华北地区(孙丽娜等,2012)多方法组合模式的回溯性检验等(Yu et al,2013,2015)。

青藏高原是我国现代最新构造活动与地震活动最强烈的地区(邓起东,2002)。喜马拉雅现代构造活动带以北,即印度板块强烈碰撞形成广阔的高原,直达祁连山以北及河西走廊地区。研究表明,这个辽阔的高原由多个板内次级断块组成,形成一幅复杂的变形图像,并与喜马拉雅构造带一起组成了一幅复杂的地震活动图像(邓起东等,2014; 张培震等,2002; 尹安,2006)。

青海地区位于青藏高原东北部,属于地震频发地带。这一区域的M≥6.0强震表现出明显的丛集特征,地震学家对于祁连地震带M≥6.0强震的预测十分关注。本文利用PI算法对青海地区3年时间尺度M≥5.0地震进行回溯性检验,对于地震前可能的地震活动“前兆性”异常进行再认识。

PI算法通过对地震活动性时空活动图像偏离“背景地震活动”情况进行分析,在中长期时间尺度上估计未来地震的概率(Rundle et al,2000b,2013)。该算法的基本原理(Tiampo et al,2002a; Nanjo et al,2005; 蒋长胜,吴忠良,2008)是对研究区域网格化处理,通过对每一个网格地震活动强度多时间尺度变化的归一化处理,检测发震显著事件概率高的网格,除去地震背景概率,得到地震危险区,即地震热点。

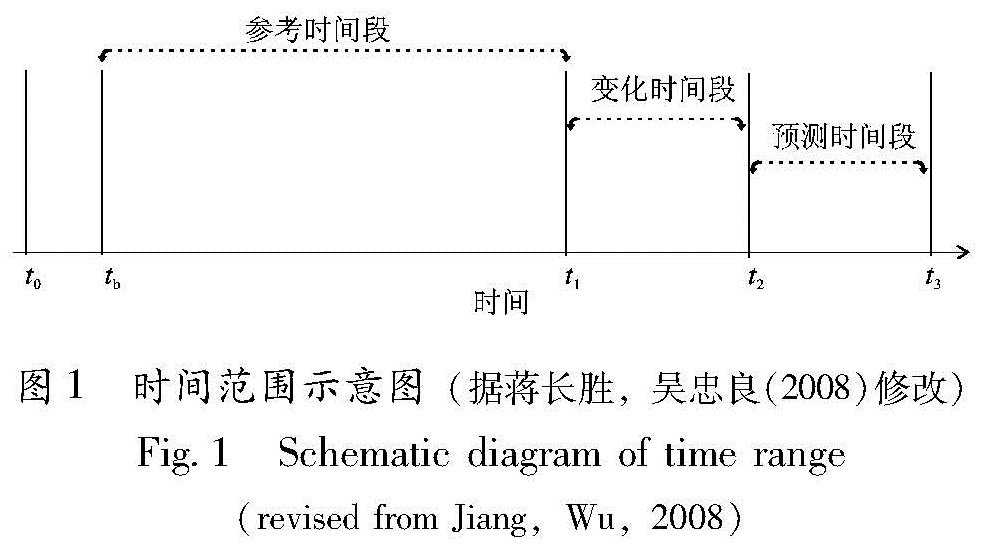
将整个地震区划分为网格,记为X_i。每一网格地震活动的时间序列N_i(t),地震须大于序列的截止震级M_C,定义的时间范围见图1。地震目录起始时刻为t₀,t_b以Δt为步长从t₀时刻向t₁时刻滑动,t₁～t₂为地震活动“异常学习”的变化时段,t₂～t₃为地震“预测时段”。

图1 时间范围示意图(据蒋长胜,吴忠良(2008)修改)
Fig.1 Schematic diagram of time range(revised from Jiang,Wu,2008)

格点i的“地震活动强度”函数I_i(t_b,t)定义为平均地震数:

I_i(t_b,t)=1/((t-t_b))∑^t_t=tbN_i(t').(1)

为对不同时间段的地震活动强度函数进行比较,将地震活动强度函数进行标准化处理,格点i处在时间间隔t_b-t的归一化统计法为

I_i(t_b,t)^-=(I_i(t_b,t)-<I_i(t_b,t)>)/(σ(t-t_b)).(2)

计算强度函数的平均变化量为

ΔIi(tb,t)^-=1/((t0-t1))∑t1tb-t0ΔIi(tb,t1,t2).(3)

未来强震发生的概率P_I(t₀,t₁,t₂)设为强度函数平均变化量的平方,强震发生在第i个网格内的概率为该网格的概率值减去所有网格概率的平均值:

ΔP_i(t₀,t₁,t₂)=P_i(t₀,t₁,t₂)-<P_i(t₀,t₁,t₂)>.(4)

其中,<P_i(t₀,t₁,t₂)>为所有网格发生地震概率的平均值。将ΔP_i(t₀,t₁,t₂)>0的网格(地区)定义为地震热点。回溯性研究的PI预测图像中,地震发生的空间危险性概率值用对数形式Lg(ΔP/ΔP_max)表示。

采用ROC方法(Swets,1973; Molchan,1996)进行PI算法预测效果的检验。ROC曲线每点表示设定的危险性概率阈值下预测结果的“命中率”和 “虚报率”,ROC曲线包含的面积越大,预测效果越好(蒋长胜等,2009)。

本文研究区为青海省及其邻区(32°～41°N,88°～103°E),该区域自北至南依次为祁连断块、东昆仑—柴达木断块、巴颜喀拉断块和羌塘断块,是中国大陆地震活动强烈的地区之一。使用1970～2015年中国地震台网中心和青海省地震局提供的地震目录。根据G-R统计,将选取地震资料的截止震级(M_C)设定为M_L3.0,预测的目标地震震级(M_F)设定为M≥5.0,这符合截止震级至少小于预测目标震级2个震级单位的条件(Holliday et al,2005a,b)。

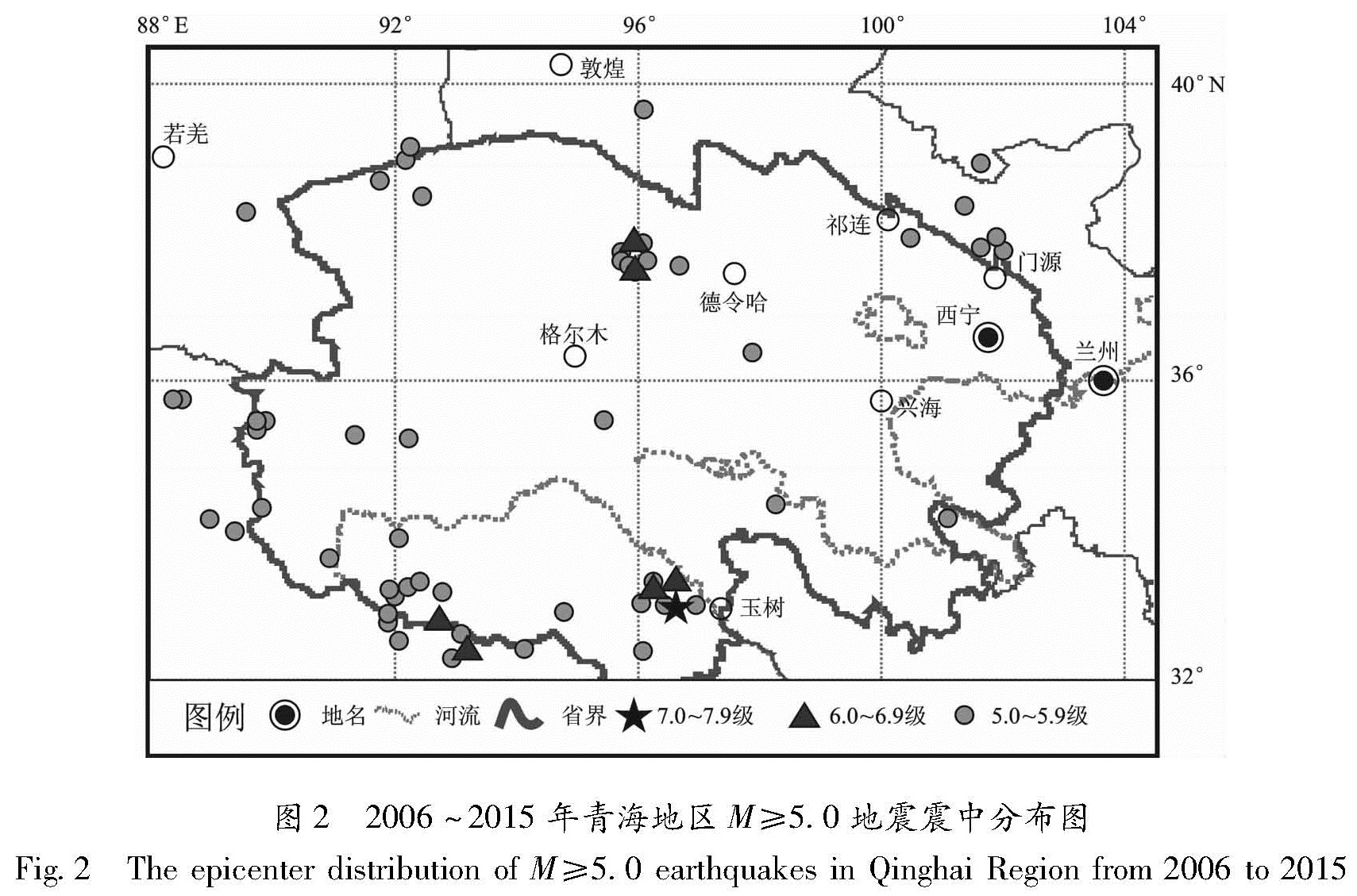
2006～2015年青海地区共发生M≥5.0地震45次(表1,图2),其中M≥7.0地震1次(2010年4月14日玉树M_S7.1地震),M≥6.0地震6次,M≥5.0地震38次。M≥5.0地震震中位置主要分布在青海南部的唐古拉、玉树地区和北部的祁连、德令哈、茫崖地区(图2)。

基于青海地震台网发展的不同阶段划分,采用G-R关系的交互式分析方法,进行1980～2015年青海地区地震目录完整性最小震级的拟合分析(图3),计算得到震级为M_L3.0时G-R拟合相关系数较高。青海地区不同时间段、不同区域地震目录的最小完整性震级存在明显差异(王培玲,胡玉,2014; 屠泓为等,2010)。2007年青海数字地震台网运行以来,全省地震台网密度逐步增大,2008年唐古拉地区架设地震监测台站5个,很大程度提高了该区域地震监测能力,青海地区地震目录完整性最小震级达到2.0。考虑到青海地区不同时间段、不同区域地震监测能力的较大差异,研究区域内M_L≥3.0地震具有较好的完备性,因此将截止震级(M_C)设定为M_L3.0。

特别需要指明,本文中没有删除地震目录中的余震序列。依据前人的统计检验结果,PI算法中余震没有从地震目录中去除掉,是认为主震后的余震发生,反映了附近区域的高应力状态(Tiampo et al,2002b)。

图2 2006～2015年青海地区M≥5.0地震震中分布图
Fig.2 The epicenter distribution of M≥5.0 earthquakes in Qinghai Region from 2006 to 2015

表1 2006～2016年青海地区M≥5.0地震参数
Tab.1 The parameters of M≥5.0 earthquakes in Qinghai Region from 2006 to 2016

图3 1980～2015年青海M≥1.0地震G-R关系图(a)1980～1989年;(b)1990～1999年;(c)2000～2008年;(d)2008～2015年
Fig.3 G-R relation of M≥1.0 earthquakes in Qinghai Region from 1980 to 2015

空间上,地震相对显著危险区域,即“热点”,热点值为ΔP_i(t₀,t₁,t₂),强度函数经归一化处理,用对数Lg(ΔP/ΔP_max)值表示,值越大,表示地震危险程度越高。

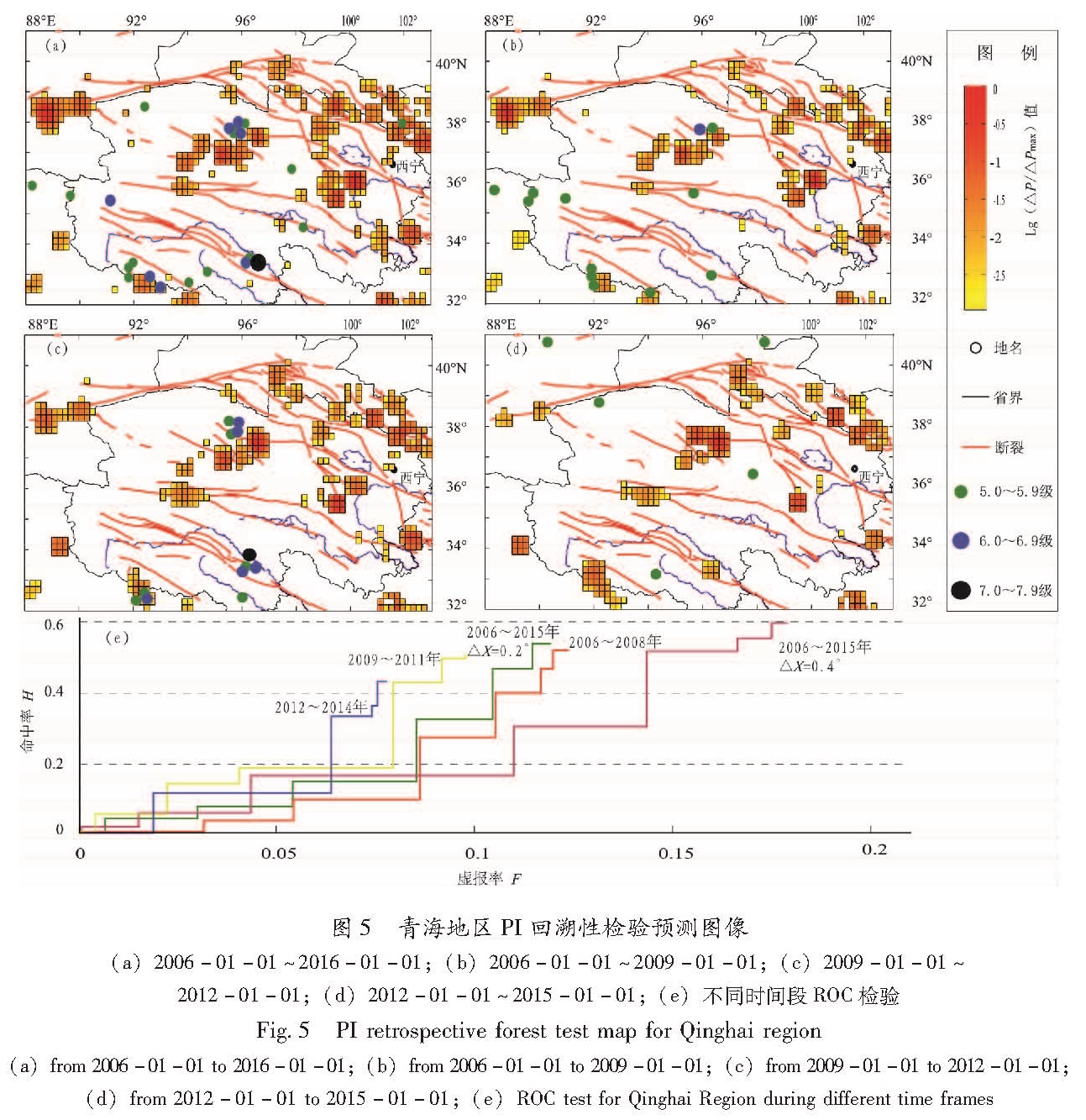
青海地区是中强地震频发区域,本文对该地区2006～2015年M≥5.0地震进行系统的回溯性检验研究,总结震前PI图像异常变化特征。对2006～2015年M≥5.0地震的命中率情况进行回溯性检验(图4),选定t₀为1970-01-01,t₁为1996-01-01,t₂为2006-01-01,t₃为2016-01-01,选取滑动窗长为30天,网格划分为0.2°×0.2°和0.4°×0.4°,截止震级(M_C)为3.0,目标震级(M_F)为5.0。从图5a可以看出,2008年和2009年青海德令哈6.3级、6.4级地震,2008年青海唐古拉地区5.1级地震,2008年甘肃肃南5.0级地震,2010年西藏那曲地区聂荣县5.7级地震均位于PI预测图像的“地震热点”区域。

通过改变网格划分尺度(ΔX=0.2°,0.4°)来分析不同空间尺度下,未来10年时间的预测效能(图5a)。从回溯性检验结果看,相同条件下网

图4 2006～2018年M≥5.0地震时间序列图
Fig.4 Time-series graph of M≥5.0 earthquakes from 2016 to 2018

格尺度ΔX=0.2°的回溯性检验结果较好,虚报率(F)为0.115时,命中率(H)为0.535 7。

考虑到PI预测结果与青海地区年度会商时间尺度相一致,本文尝试使用10年时间尺度的地震活动异常“变化学习”时间段和3年时间尺度的“预测”时间段分别进行统计。选取滑动窗长为30天,网格划分为0.2°×0.2°。选定t₀为1970-01-01,分别选取t₂时刻为2006-01-01、2009-01-01和2012-01-01共3个回溯性“预测时间段”,以及t₂为2016-01-01的1个“向前”预测时间段。每个预测时间段为3年时间尺度,不同回溯性时间段PI预测图像分别为见图5b、c、d。由图可见,“预测时间段”内的强震与PI图像的地震热点有较好的对应关系。采用ROC方法计算预测效果,如图5e所示,2006～2008年和2009～2011年2个回溯性“预测时间段”评价效果较好。但2012～2014年预测时间段“命中率H”低于0.5,呈现热点多、虚报率高的特点。分析其原因,2012～2014年M≥5.0地震多发生于青海地区周边,PI预测图像可能与选择研究区域有密切关系。

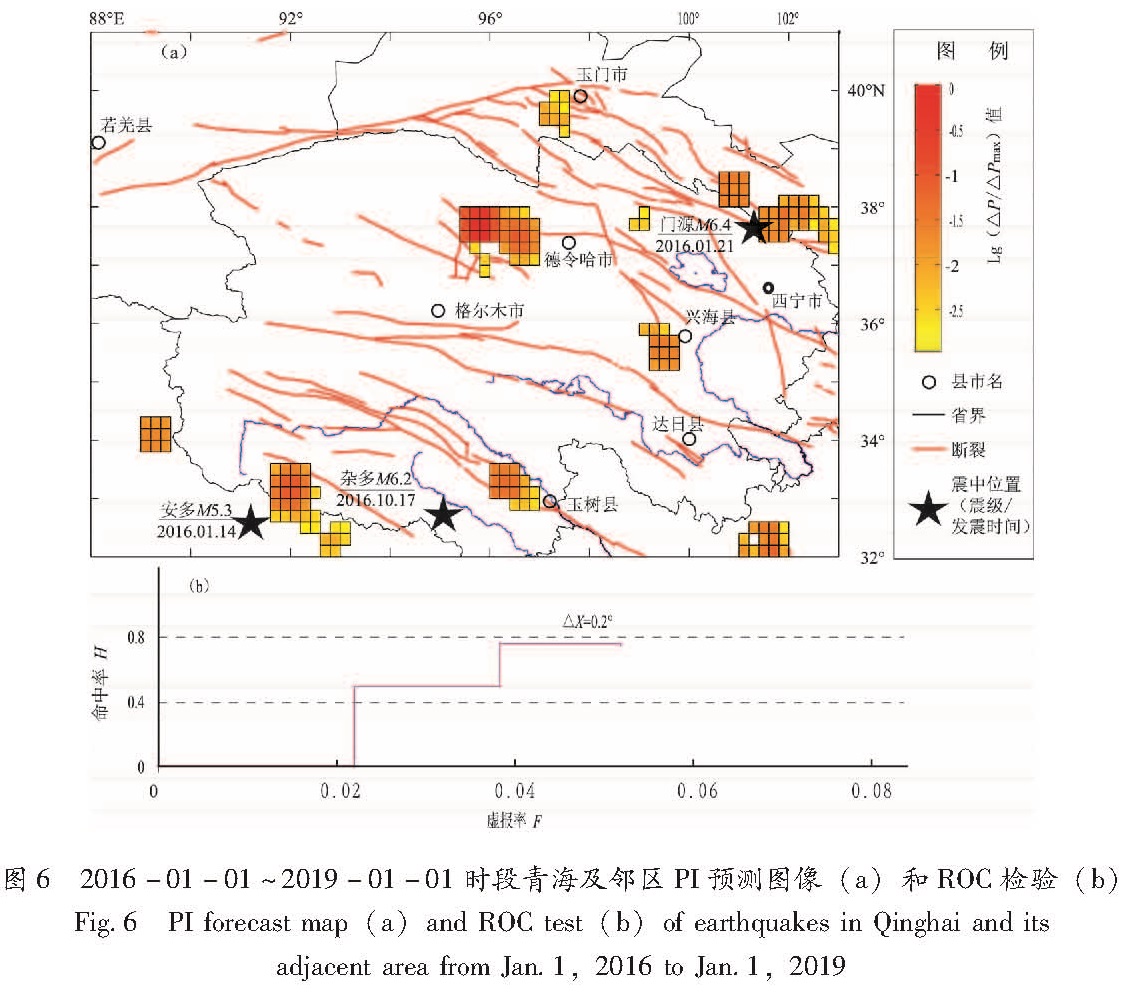
为研究青海地区未来3年地震可能的发生地点,“向前”预测3年(2016～2018年)时间段M≥5.0地震,选定t₀为1970-01-01,t₁为2006-01-01,t₂为2016-01-01,t₃为2019-01-01,选取滑动窗长为30天,研究区空间网格划分为0.2°×0.2°,截止震级(M_C)为3.0,目标震级(M_F)为5.0。“异常学习”时间段为10年(2006～2015年),青海及邻区3年尺度预测时间段(2016～2018年)的PI图像如图6a所示,结果显示,未来3年内热点值相对较高区域为门源—祁连、德令哈、兴海、玉树、唐古拉等地区。

图5 青海地区PI回溯性检验预测图像(a)2006-01-01～2016-01-01;(b)2006-01-01～2009-01-01;(c)2009-01-01～2012-01-01;(d)2012-01-01～2015-01-01;(e)不同时间段ROC检验
Fig.5 PI retrospective forest test map for Qinghai region (a)from 2006-01-01 to 2016-01-01;(b)from 2006-01-01 to 2009-01-01;(c)from 2009-01-01 to 2012-01-01;

从图6a可以看出,地震热点多集中在地震多发区域,如祁连、德令哈、唐古拉等地区,这反映了历史地震对于PI算法的变化时间段和预测时间段有重要影响,历史上均有大地震发生,并且现阶段是中、小地震频发区域。

3年预测时间段(2016～2018年)内,截至2016年10月28日,青海省及邻区共发生M≥5.0地震3次,图6a中黑色五角星为3次地震震中位置。其中,最大为2016年1月21日门源M_S6.4地震。青海门源M_S6.4、西藏安多M_S5.3地震位于PI图像的地震热点丛集附近,反映了“PI图像热点”具有较好的地点预测能力。

因预测时间尚未结束,3年预测时间段(2016～2018年)内,ROC检验只计算到2016年10月28日,显示较好的ROC评价结果(命中率达到0.75,如图6b所示)。

本文选取10年尺度的地震活动“变化学习”时间段,3年尺度的“预测”时间段,0.2°×0.2°空间网格及截至震级M_L3.0进行统计计算。通过对3个回溯性“预测时间段”和1个“向前”预测时间段分析,结果表明,PI算法适用于青海及邻区中强地震的中长期预测。2016年青海门源M_S6.4和西藏安多M_S5.3地震与附近较大范围显著

图6 2016-01-01～2019-01-01时段青海及邻区PI预测图像(a)和ROC检验(b)
Fig.6 PI forecast map(a)and ROC test(b)of earthquakes in Qinghai and its adjacent area from Jan.1,2016 to Jan.1,2019

的高概率危险“热点”相对应,ROC评价效果较好。

PI图像预测结果显示,未来3年(2016～2018年)门源—祁连、德令哈、兴海、玉树、唐古拉地区地震热点值偏高。

对青海地区南部的高概率“热点”性质进行讨论,青海南部地区与北部地区相比较,具有“热点”分散、漏报率高的特点。如漏报的2016年10月17日杂多M_S6.2地震,位于2个地震“热点”危险区之间,漏报地震还包括2010年4月14日玉树M_S7.1地震。分析地震漏报的现象,可能受到以下2方面的影响:一是历史上青海南部的唐古拉地区本身地震监测能力较弱,2008年之后地震监测点密度加大,监测能力才有了逐步提升。用ROC检验来评估预测效能,该检验为不全面的“单向性”检验过程,仅验证新发生的地震是否在PI图像的地震“热点”区域附近。对于历史上发生较多“目标地震”的区域,ROC检验才具有较好的评估效能。二是考虑青藏高原应力应变场影响因素,应力场的分布对运动场起着极为重要的作用,运动速度大致由南向北逐渐减小(郑勇等,2007)。青海南部地区地震存在较多“漏报”的PI图像“热点”,从PI算法本身很难解释出具体原因,一种可能的解释是青藏高原南部区域的运动速率较大,PI算法在运动速率较大的板块边缘地区比较难得到“目标地震”的图像“热点”,可能需要在PI图像“热点”的计算过程中,把应力应变场作为一个影响因素考虑在内。