基金项目:地震科技星火计划项目“基于b值和波形动态分析序列特征”,国家重点研发计划项目(2021YFC3000705)和台网青年项目“强震危险地点预测方法研究——以南北地震带为例”联合资助.
(China Earthquake Networks Center,Beijing 100045,China)
inferred magnitude of the largest aftershock; b-vaule; the North-South Seismic Belt; aftershock sequences; the Gutenberg-Richter law
DOI: 10.20015/j.cnki.ISSN1000-0666.2022.0042
备注
基金项目:地震科技星火计划项目“基于b值和波形动态分析序列特征”,国家重点研发计划项目(2021YFC3000705)和台网青年项目“强震危险地点预测方法研究——以南北地震带为例”联合资助.
引言
我国的国土面积虽仅占全球陆地面积的7%,却有全球33%的大陆强震发生在我国(中国地震信息网,2018)。据中国地震信息网(2018)统计,1901—2001年我国大陆因地震死亡人数达到60余万人,最惨烈的是1920年12月宁夏海原8.6级地震和1976年7月河北唐山7.8级地震,死亡人数分别是23.55万人和24.2万人。20世纪以来,科技得到了迅速的发展,但是从发震频度上看,1950年以来中国大陆地区平均每年发生5级地震24次、6级地震4次、7级地震0.6次,地震仍然是人民生命安全和社会发展的巨大威胁。
南北地震带作为中国大陆中部强震相对密集分布的地震带,发生了2008年四川汶川MS8.0、2010年青海玉树MS7.1、2013年四川芦山MS7.0、2017年四川九寨沟MS7.0、2014年云南景谷MS6.6、2014年云南鲁甸MS6.5等一系列强震,这些强震对震中及其附近城市和乡镇均造成了巨大的伤害。例如截至2008年9月25日,2008年汶川MS8.0地震共造成直接经济损失8 523.09亿元,致使69 227人死亡,17 923人失踪以及374 643人受伤(陶正如,陶夏新,2021)。研究显示南北地震带仍存在发生强震的可能(M7专项工作组,2012)。
强震发生后,快速研判该地震序列的类型及余震强度具有重要的减灾意义。现阶段我国震后应急及地震序列跟踪工作中,针对地震序列类型及余震强度的判定方法,以震中附近历史地震序列对比分析为主,并综合考虑统计规律(中国地震局监测预报司,2007; 吕晓健等,2010; 蒋飞蕊等,2015; 赵小艳等,2021)、h值(刘正荣,孔昭麟,1986; [HJ2.1mm]马茹莹等,2016)以及推定最大余震震级方法(吴开统等,1984; Shcherbakov,Turcotte,2004)等的计算结果。其中推定最大余震震级方法可以依据地震序列数据实时评估最大余震震级,且计算简单快速,是震后评估最大余震震级水平的常用方法之一。Shcherbakov等(2013)利用该方法估算了全球70个俯冲带地震序列的最大余震(或最大后续地震)震级,结果显示对于大多数序列可以准确估计出最大余震震级,对于震级差为0.2级的震群序列也可以有效估计出最大后续地震震级。苏有锦等(2014)针对全球184个7级以上浅源主-余型地震序列研究了震后不同时间下推定最大余震震级方法的适用性,结果显示估算出的最大余震震级与实际值的差值多为-0.5~0.5,且可以利用震后短时间尺度的余震数据估算出合理的最大余震震级。解孟雨等(2017)基于九寨沟7.0级地震序列的数据,讨论了震级类型、余震目录时间长度对于推定最大余震震级方法的影响,结果显示该方法对面波震级MS和里氏震级ML均适用,且余震目录时间尺度较长时,最大余震震级估算值较好,利用震后短期的计算结果也可以作为最大余震震级的合适估计。
[BW(S][BG(; N][BHDWG1*2,WK15mmZQ,WK140mm,WK15mmYQW][][HT5"][CM(22mm]地震研究[CM)][]45卷[BG)F][BW)][BW(D][BG(; N][BHDWG1*2,WKZQ0W][HT5"]第3期解孟雨等:推定最大余震震级法在南北地震带的应用[BG)F][BW)]为进一步分析推定最大余震震级方法对我国大陆地区强震序列的有效性,分析不同常用最小完备震级和b值计算方法组合下的估算结果,本文针对南北地震带开展相关研究,选取该区2000—2020年MS≥6.0地震序列数据,讨论分析不同方法组合以及数据时间长度对实际最大余震震级的影响,然后依据分析结果提出了最优的推定最大余震震级方法。
1 计算方法
对于现有的地震序列记录,一般满足G-R定律,即:
lg N(≥M)=a-bM (1)
式中:N(≥M)为震级大于M的余震个数; a和b则是正常数,a描述了选定区域地震活动性水平的高低程度,它依赖于选定区域和观测数据时间尺度的大小,一般认为a值给出了区域总的地震个数,而b值刻画了区域内地震大小的相对分布情况,其范围为0.6~1.4(Marzocchi,Sandri,2003; Shcherbakov,Turcotte,2004; Wang et al,2015; Hamdache et al,2017)。N=1时,地震序列的推定最大余震震级为:
MILA=a/b (2)
从式(2)可以看出,只需在地震序列最小完备性震级MC的基础上,计算出参数a和b,便可估算序列最大余震震级,这一方法就称为推定最大余震震级法。
最小完备性震级MC的估算方法主要分为两类(Mignan,Woessner,2012):基于台站的方法和基于目录的方法。基于目录的方法相对简单明确,适合实现快速计算,其中最大曲率法(MAXC)和拟合优度测试法(GFT)计算较为简单快捷,满足震后最大余震震级快速评估的要求。
MAXC将地震个数N(M0+dM≥M≥M0)最大时对应的震级M0值作为地震目录的MC,其中dM为地震震级记录的最小间隔,一般为0.1。MAXC会低估地震目录的MC,因此更为接近实际真值,一般会添加修正系数0.2,即MC=MC(MAXC)+ 0.2(Woessner,Wiemer,2005),该计算方法称为修正MAXC。
GFT首先定义了衡量拟合G-R定律曲线与实际数据拟合程度的参数R值:

式中:MCO为选定的震级; a、b为针对M≥MCO地震目录计算出的参数值; Bi和Si分别为每一震级档下观测到的累积地震个数和按拟合G-R定律计算出的累积地震个数。通过改变MCO大小,计算出相应的R值,当R值大于设定阈值时,MCO取为地震目录的MC。通常R值阈值设定为90%或95%,相应的MC一般记为MC-90和MC-95。使用GFT估算MC时,存在无法计算出MC-90和MC-95的情况,因此在实际使用过程中常采用GFT和修正MAXC的混合方法,依次确定是否可以计算出MC-95和MC-90,如果都无法计算出,则利用修正MAXC计算相应的MC(Wiemer,2001)。
b值的计算方法主要分为两大类:最小二乘法和最大似然法。对于最小二乘法(LS),本文采用常用的线性回归系数最小二乘估计(贾俊平等,2018),即设定变量x和y之间满足:
y=β0+β1x+ε (4)
式中:β0和β1为需要确定的常数; ε为误差项,反映了除x和y之间线性关系的其他因素的影响。由实测数据x和y可以得到β0和β1的估计值分别为:
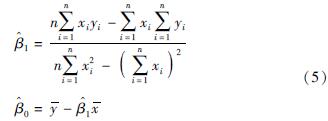
式中:n为实测数据的个数; x和y分别为实测x和y的均值。b值计算时,式(4)中x为震级M,y为余震个数N的常用对数lgN,β0为a,β1为-b,通过式(5),即可估算出a和b。同时为了使G-R定律拟合效果最佳,计算过程中通过改变震级上限,选取拟合值和实测值之间误差最小的拟合参数作为最终计算结果。
使用最大似然法(ML)估算b值,常用的b值及不确定度δb计算如下:

式中:M[TX-]为计算地震目录的平均震级; Nt为计算目录中事件的总个数(Marzocchi,Sandri,2003)。Marzocchi和Sandri(2003)通过对比式(6)与其他最大似然法的计算结果,进一步指出利用式(6)可对较大的b值进行有效估算,在地震震级存在误差的情况下,仍然可以有效地估算b值。同时a值为(吴果,2018):
a=lg [N(≥MC)]+bMC (8)
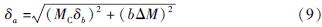
在采用ML计算b值时,M≥MC的地震总数N(M≥MC)必须足够大,一般为N≥30(Aki,1965; 贾俊平等,2018)。
为了寻找最优的组合方法,本文采用上述常用方法的组合计算出推定最大余震震级MILA,然后通过对比分析MILA对实际最大余震震级MRLA的估算效果,确定更为有效的方法组合。具体而言,分别采用修正MAXC方法以及GFT和修正MAXC的混合方法(以下分别简称为MAXC和GFT)计算MC,然后分别使用LS和ML计算b值,构成4种最大余震震级估算方法组合,即GFT+LS、GFT+ML、MAXC+LS和MAXC+ML。
为评价最大余震震级估算效果以及对比各种组合方法的结果,本文使用误差均值
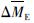 和误差变异系数CM。首先计算出主震后不同时刻最大余震震级估算的误差ΔME,然后分别计算出不同主震后同一时刻
和误差变异系数CM。首先计算出主震后不同时刻最大余震震级估算的误差ΔME,然后分别计算出不同主震后同一时刻 和CM,其中
和CM,其中 越小,表示MILA和MRLA越接近,估算结果越准确; CM则用于比较不同组合方法误差的离散程度(贾俊平等,2018),CM越小则表明误差值越集中,说明估算方法对于不同序列更为稳定,更适合估算不同地震序列的最大余震震级。
越小,表示MILA和MRLA越接近,估算结果越准确; CM则用于比较不同组合方法误差的离散程度(贾俊平等,2018),CM越小则表明误差值越集中,说明估算方法对于不同序列更为稳定,更适合估算不同地震序列的最大余震震级。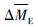 和CM的计算公式分别为:
和CM的计算公式分别为: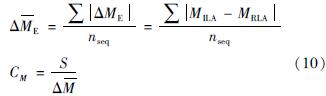
式中:nseq为地震序列总个数; S为误差的标准差。
2 数据和结果
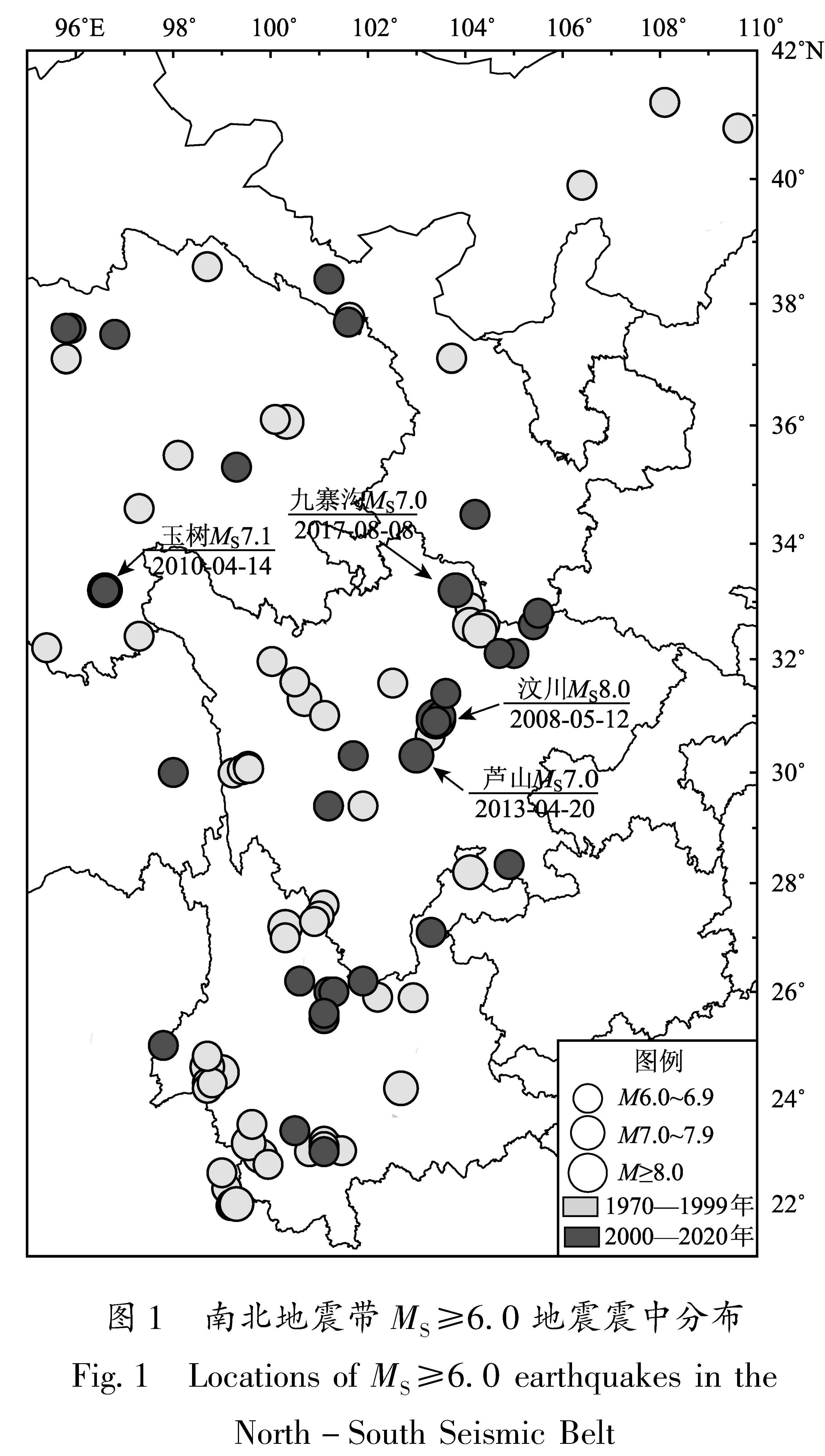
南北地震带是一条由不同方向、不同性质断裂和褶皱构成的近南北向的复杂构造带和地震活动带,是中国大陆地震活动最为强烈的地区之一。依据地质构造特征和地震活动的空间分布特征,可以给出南北地震带不同的空间范围定义。为收集足够的地震序列数据,同时也为大震活跃区地震序列最大余震的评估提供可行的手段,本文采用以中国大陆强震的空间分布特征定义的南北地震带范围(邵志刚,张浪平,2013),即(21°~45°N,95°~110°E)。在该研究范围内,2000—2020年中国地震台网目录中共记录到6级及以上地震35次,其中MS6.0~6.9地震31次,MS≥7.0地震4次,去掉余震后共有25个MS≥6.0地震(表1、图1)。由于2000年1月15日姚安6.5级、2000年9月12日兴海6.6级、2001年10月27日永胜6.0级以及2008年11月10日海西6.3级地震序列的现有目录存在记录时间较短、地震个数较少或缺失小震的情况,无法进行推定最大余震震级的计算,因此仅对其余21个地震序列进行研究。
蒋海昆等(2007)指出绝大多数5.0级以上
地震序列的最大余震发生生在震后1a内,其中93%的最大余震发在震后90 d内。在日常震后趋势研判中,我们更关注震后90 d内的最大余震震级。因此针对南北地震带21个MS≥6.0地震序列,本文分别使用4种MC和b值的方法组合,分别估算主震后1、3、5、7、15、30、90 d时的最大余震震级,然后与震后90 d内实际发生的最大余震震级进行对比。
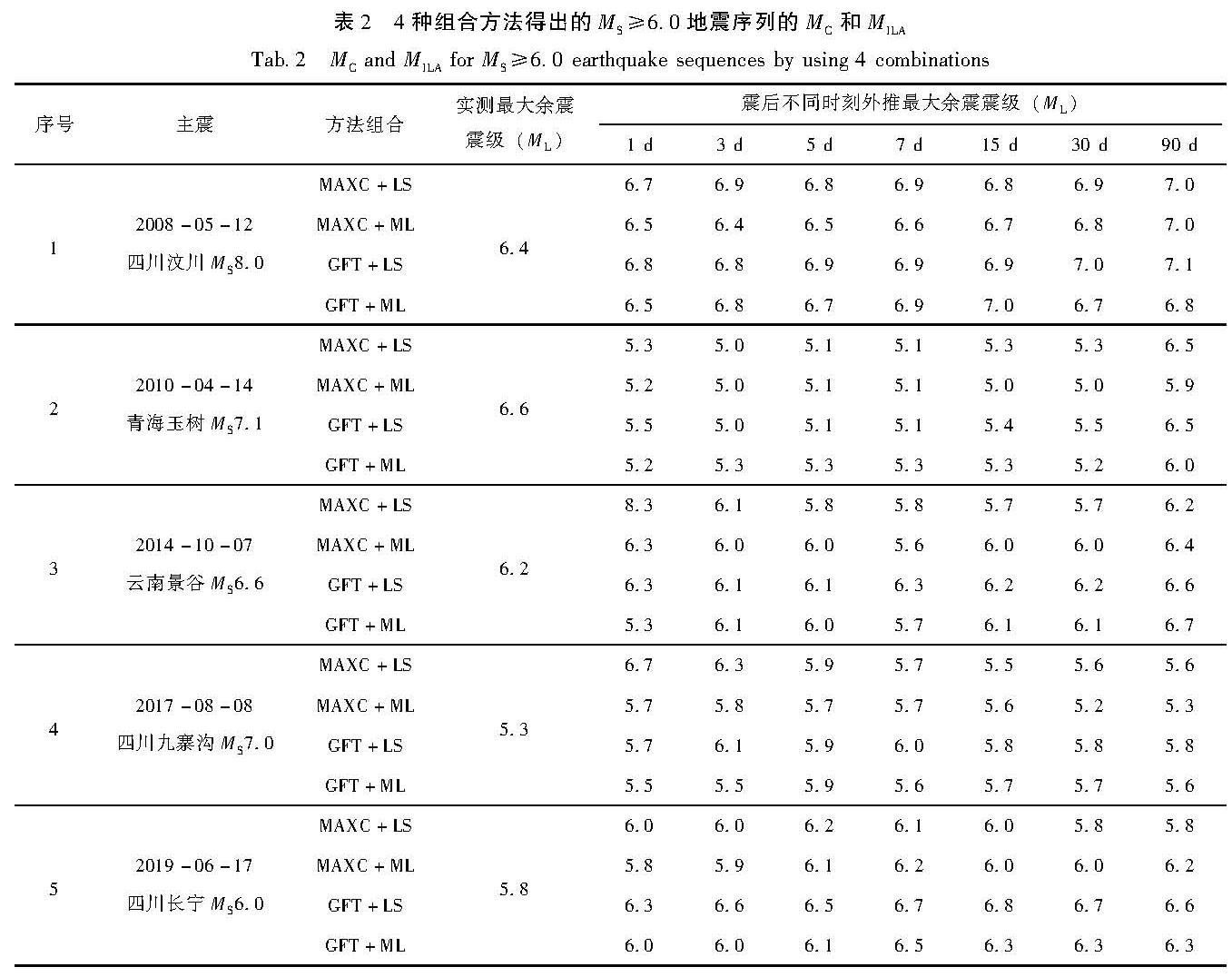
图2为使用4种组合方法计算出的21个地震序列发生后不同时刻推定的最大余震震级所对应的ΔM[TX-]E和CM。从整体上看,ΔM[TX-]E主要在0.5~1。在主震发生后早期,ΔM[TX-]E变化较大且值也较大; 随着时间推移,余震逐渐增多且余震发生率逐渐衰减,ΔM[TX-]E逐渐减小并趋于稳定,接近于0.5, 显示推定最大余震震级方法可以给出合理的最大余震震级估算值。表2中不同震级档主震序列的计算结果显示,使用推定最大余震震级方法给出的估计值与使用的余震目录时长没有明显的比例关系,显示出余震序列演化的复杂性。
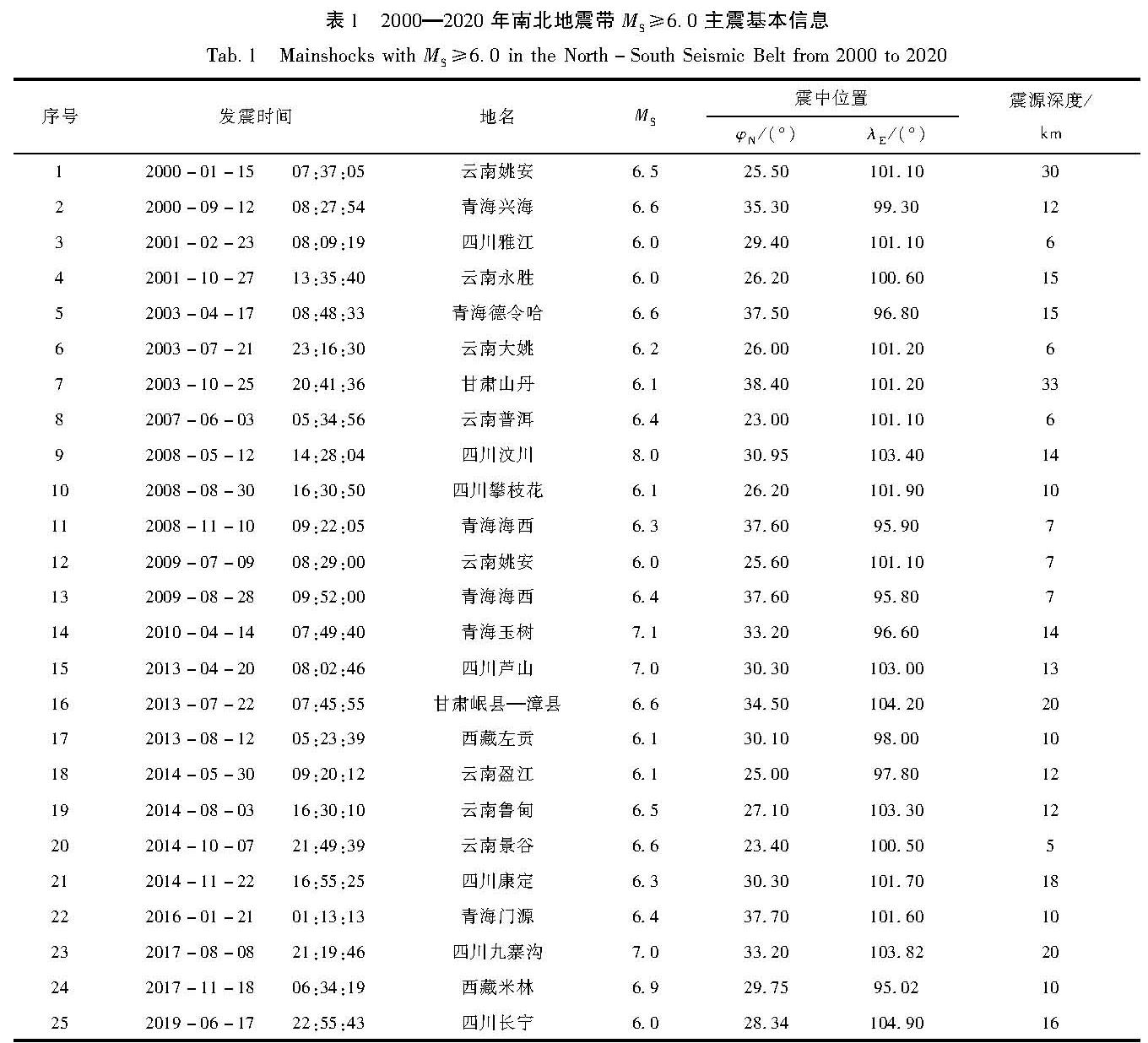
表1 2000—2020年南北地震带MS≥6.0主震基本信息
Tab.1 Mainshocks with MS≥6.0 in the North-South Seismic Belt from 2000 to 2020图1 南北地震带MS≥6.0地震震中分布
Fig.1 Locations of MS≥6.0 earthquakes in the North-South Seismic BeltMC计算方法的选择对震后15 d内最大余震震级有一定的影响,对震后15~90 d结果的影响较小,选择GFT方法计算MC时,估算结果相对更准确和稳定。具体而言,当b值估算[HJ1mm]方法为LS时,使用MAXC方法计算得出的ΔM[TX-]E值明显大于使用GFT方法得出的ΔM[TX-]E值(图2a); 同时也出现了如2014年景谷MS6.6地震震后1 d ΔM[TX-]E显[HJ2.1mm]著超过0.5,甚至达到2.0的现象(表2),表现出较差的估算效果; MAXC+LS组合方法的CM也相对较大,显示出更低的方法稳定性(图2b)。当b值估算方法为ML时,虽然震后15 d内使用不同MC计算方法得到的最大余震震级[HJ1mm]存在一定差异,但差异较小,震后15 d得到的ΔM[TX-]E基本[HJ2.1mm]一致,CM曲线也基本一致,这表明选择ML估算b值时,MC计算方法的选择对最大余震震级估算值影响较小。
对于b值计算方法的影响,图2显[HJ1mm]示在震后30 d内ML方法对应的ΔM[TX-]E值明显小[HJ2.1mm]于LS方法,更接近0.5,在震后30 d后二者相差较小。震后30 d内,当MC计算方法为GFT时,选择LS方法时CM相对较小,但差异不大,在0.1左右; 而MC计算方法为MAXC时,选择LS时CM较大,明显大于ML的对应值。总体上,除MAXC+LS组合方法得出的CM在震后30 d内相对较大,其他3种组合方法得出的CM相差较小,表明稳定性基[HJ1mm]本一致。综上分析,可以得出选择GFT+ML方法时,ΔM[TX-]E值更[HJ2.1mm]小,相应最大余震震级的估算结果更为准确,同时该方法与其他组合方法的稳定性相当。
图2 4种组合方法得出的ΔM[TX-]E(a)和CM(b)
Fig.2 ΔM[TX-]E(a)and CM(b)curves resulted from 4 combinations表2 4种组合方法得出的MS≥6.0地震序列的MC和MILA
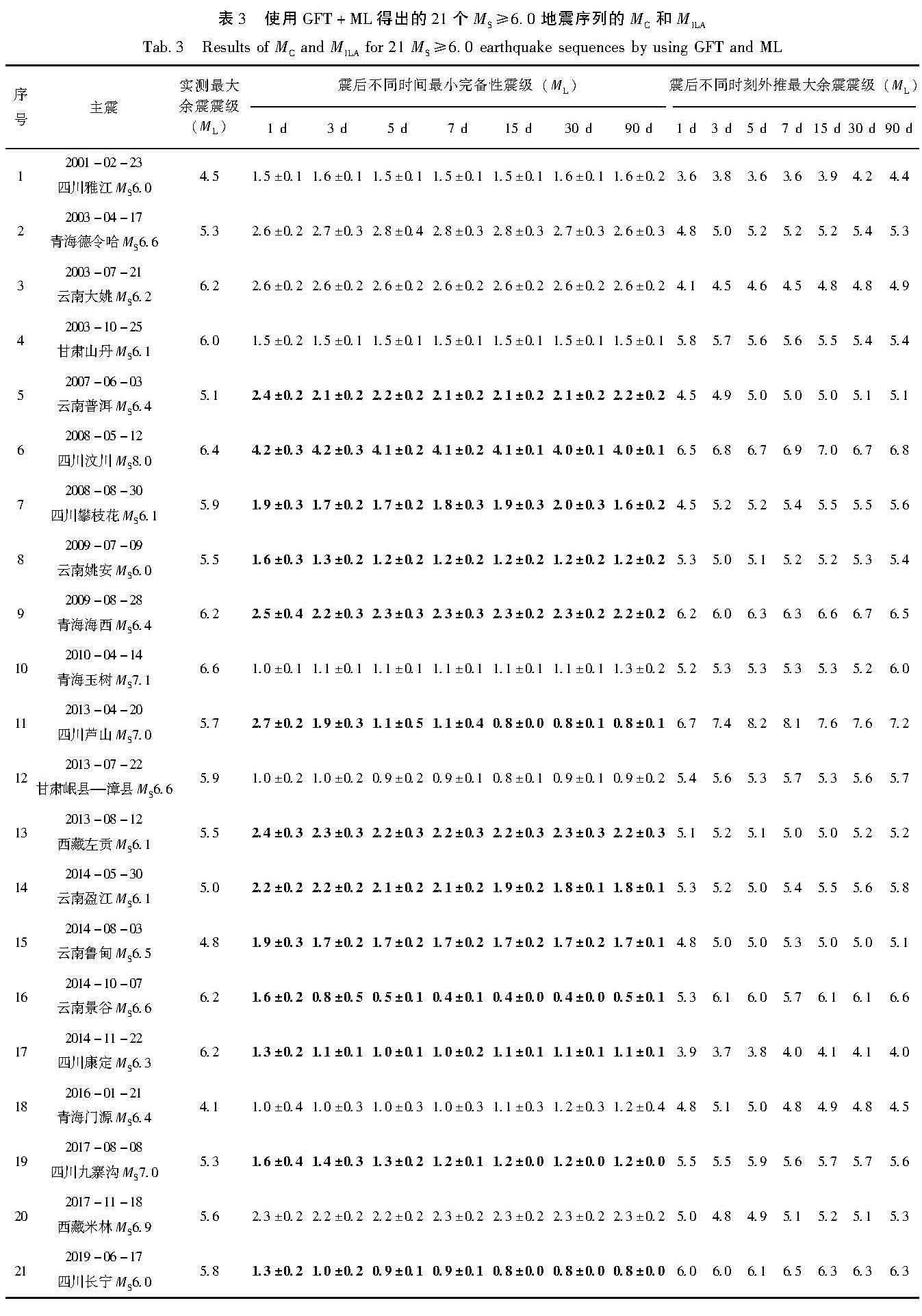
Tab.2 MC and MILA for MS≥6.0 earthquake sequences by using 4 combinations表3进一步给出了使用GFT+ML组合方法得出的21个MS≥6.0地震序列在震后不同时刻的MC和最大余震震级MILA的估计值。2013年芦山MS7.0、2019年长宁MS6.0等13个地震序列的MC随时间增加而逐步减小(表3中加粗的数字),符合通常的预期,而其他序列的MC则随时间增加基本不变或者呈现小幅波动变化。2010—2020年多数MS≥6.0地震序列MC<ML2.0,这可能是由于南北地震带台网的升级和布设使得MC出现了整体的下降。震后不同时刻的MILA整体上与余震数据时间长度不存在明显的比例关系。如果定义误差绝对值[JB<1|]ΔME[JB>1|]≤0.5为方法估计结果正确,则有约71.4%(15/21)的地震序列可以在震后90 d时获得正确的估计结果,同时有57%(12/21)的地震序列可以在震后1 d内给出正确的估计值,以上表明用GFT+ML组合估算最大余震震级有较好的正确率,利用震后短期的数据进行最大余震震级的估计,也具有一定的正确率。
3 讨论
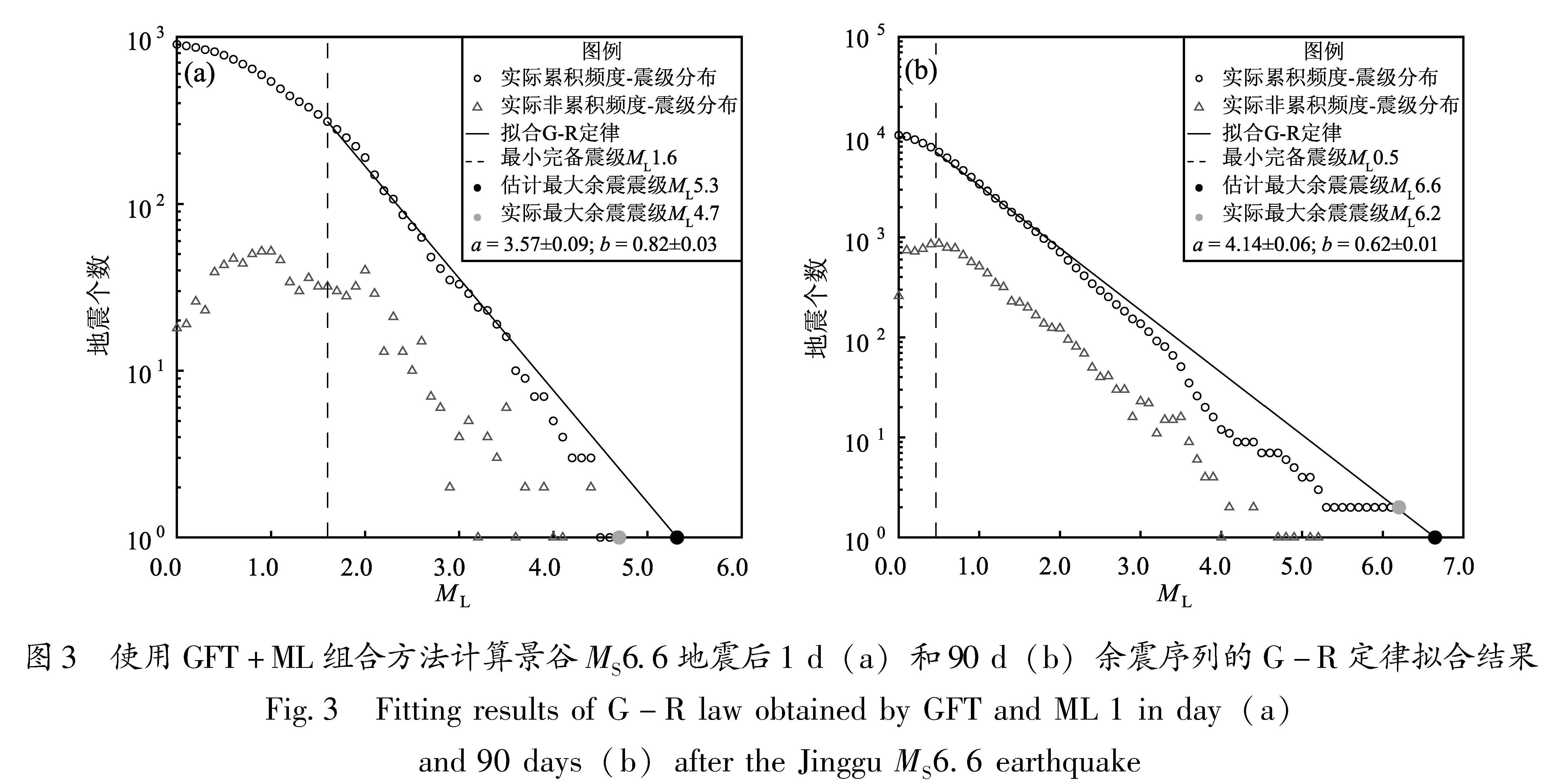
为进一步说明ΔME随时间变化的可能原因、LS改进方法的效果以及导致LS和ML方法计算ΔM[TX-]E值存在差异的可能原因,本文以2014年云南景谷MS6.6和2001年四川雅江MS6.0地震序列为例,绘制出相应的G-R定律拟合结果。随着时间增大,整体上最大余震震级估计值和实际值的误差ΔME在逐步减小,同时震后短期内ΔME值相对较大,这可能是由于余震不足引起的。以2014年景谷6.6级地震为例,ΔME的绝对值在震后1 d为0.9,而在震后90 d则降低为0.4(表3和图3)。从景谷MS6.6地震后1 d的余震数据可以看出,非累积频度-震级分布斜率与拟合的G-R定律不一致,不符合以往的研究认识,即非累积频度-震级分布也服从G-R定律,且相应的b值与累积频度-震级分布给出的
表3 使用GFT+ML得出的21个MS≥6.0地震序列的MC和MILA
Tab.3 Results of MC and MILA for 21 MS≥6.0 earthquake sequences by using GFT and ML拟合值一致(Okal,Romanowicz,1994),这表明已发生的余震个数可能不足,需要随时间推移发生更多的余震以调整非累积频度-震级分布,使得最大余震震级估计值更准确。景谷地震后90 d时,随着余震的不断发生,实测非累积频度-震级分布曲线与累积频度-震级分布曲线以及拟合出的G-R定律基本平行,表明此时非累积频度-震级分布已符合G-R定律,同时相应的误差ΔME值也最小,符合之前的推测。其他地震序列的计算结果也有相似的情况。
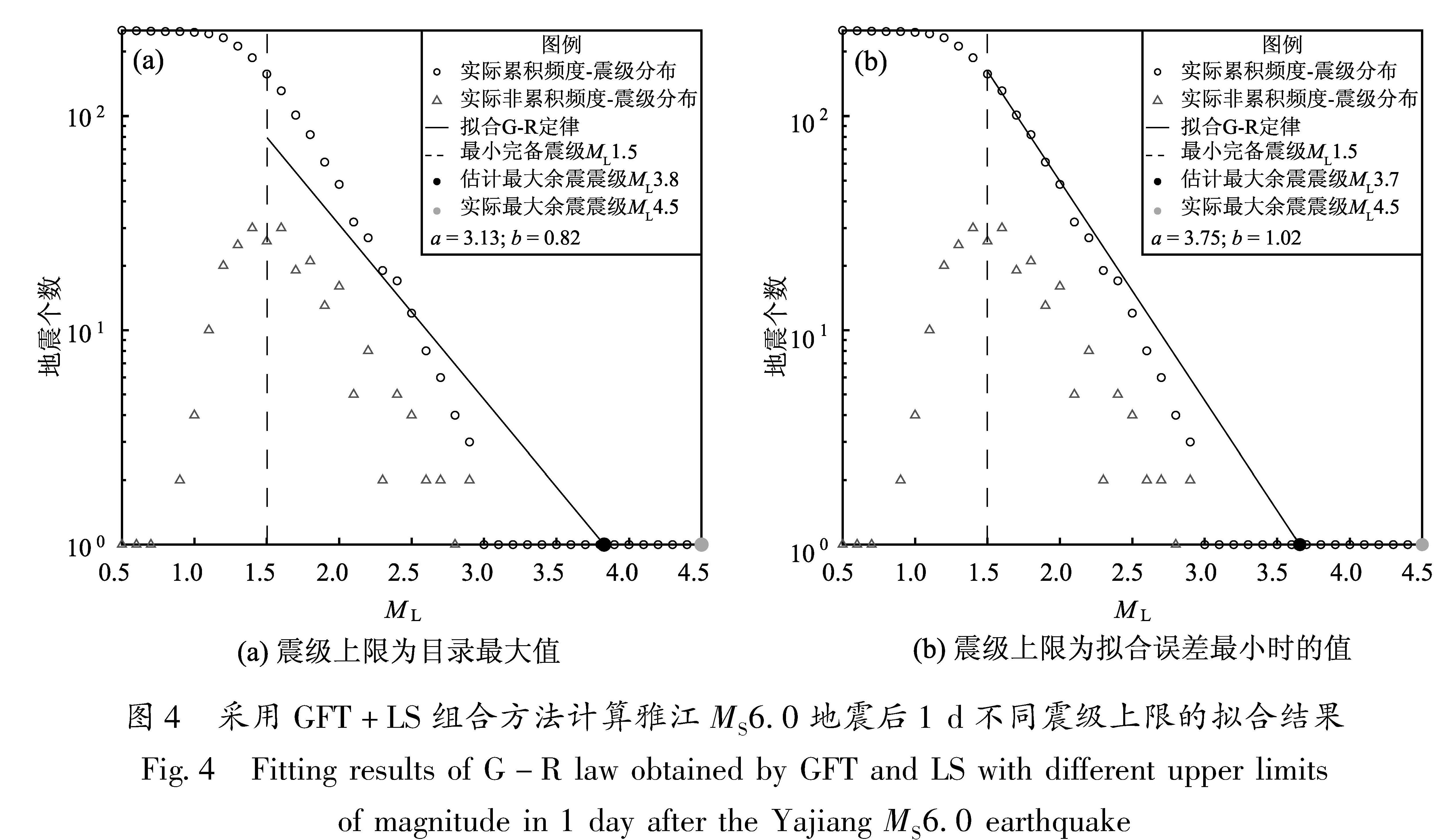
在使用LS方法计算b值时,较大震级地震的权重较大(吴果,2018),因此在计算时,若不限制余震数据的震级上限,则相应的G-R定律拟合曲线会存在偏离实测累积频度-震级分布的情况。如利用LS方法对雅江MS6.0地震后1 d的余震数据进行拟合时,如不限制震级上限,G-R定律拟合曲线存在明显的偏离(图4a),此时b值以及外推最大余震震级均不可信。而按照本文LS方法的计算方法,即自动选取拟合G-R定律和实测累积频度-震级分布误差最小时的震级上限,则可以一定程度上避免拟合曲线偏离的问题,提高拟合结果的可靠性(图4b)。
图3 使用GFT+ML组合方法计算景谷MS6.6地震后1 d(a)和90 d(b)余震序列的G-R定律拟合结果
Fig.3 Fitting results of G-R law obtained by GFT and ML 1 in day(a) and 90 days(b)after the Jinggu MS6.6 earthquake图4 采用GFT+LS组合方法计算雅江MS6.0地震后1 d不同震级上限的拟合结果
Fig.4 Fitting results of G-R law obtained by GFT and LS with different upper limits of magnitude in 1 day after the Yajiang MS6.0 earthquake整体上使用LS方法进行最大余震震级估计的结果比使用ML时的大。以景谷地震为例,震后1 d使用LS方法计算出的最大余震震级为ML8.3,远大于实际最大余震震级ML6.2(表2和图5)。对比图5和图3a可以看出,尽管采用了寻找最小误差的方法确定震级上限,部分改善了LS方法计算时较大震级地震权重较大的问题,但当小震级地震缺失时,仅考虑较小震级范围余震的拟合G-R定律会偏离考虑全部M≥MC余震时拟合出的G-R定律。Sandri和Marzocchi(2007)通过理论分析和数值计算讨论了使用LS方法估算的b值情况,结果显示理论上LS方法得到的b值会明显低于给定值。因此为了震后快速准确地估算余震序列最大地震震级,ML方法是更合适计算b值的方法。
图5 使用MAXC+LS组合方法得到的景谷MS6.6地震后1 d的G-R定律拟合结果
Fig.5 Fitting results of G-R law obtained by MAXC and LS combination in 1 day after the JingguMS6.6 earthquake4 结论
本文以南北地震带为研究区域,筛选出2000—2020年共21个MS≥6.0地震序列,使用4种组合方法GFT+LS、GFT+ML、MAXC+LS和MAXC+ML分别进行计算,得到震后不同时刻外推最大余震震级,以及该震级值对于实际最大余震震级的估算效果,得到的主要结论如下:
(1)外推最大余震震级与实际最大余震震级差值绝对值的均值ΔM[TX-]E主要为0.5~1.0,且随时间推移,ΔM[TX-]E趋于0.5,显示长时间尺度下外推最大余震震级可以较准确反映实际最大余震震级。
(2)通过分析震后不同时刻非累积频度-震级分布的特征与外推最大余震震级估计效果的关系,发现外推最大余震震级与实际最大余震震级差值ΔM[TX-]E随时间推移逐步减小,可能是因为随时间增加余震不断发生,使得非累积频度-震级分布由偏离G-R定律变得逐步符合G-R定律。
(3)通过对比各组合方法所得ΔM[TX-]E和CM的特征以及估计震级正确的比例,发现在实际应用外推最大余震震级法时,GFT+ML组合估算效果最好,具有更低的误差和较高的正确率。
-
贾俊平,何晓群,金勇进,等.2018.统计学[M].北京:中国人民大学出版社.
- 蒋飞蕊,叶建庆,杨晶琼.2015.云南地区中强地震余震序列部分统计特征分析[J].华北地震科学,30(4):37-44.
- 蒋海昆,郑建常,吴琼,等.2007.中国大陆震中强以上地震余震分布尺度的统计特征[J].地震学报,29(2):151-164.
- 解孟雨,孟令媛,申文豪,等.2017.基于Gutenberg-Richter定律快速估算最大余震震级:以2017年九寨沟MS7.0地震为例[J].中国地震,33(4):493-502.
- 刘正荣,孔昭麟.1986.地震频度衰减与地震预报[J].地震研究,9(1):1-12.
- M7专项工作组.2012.中国大陆大地震中-长期危险性研究[M].北京:地震出版社.
- 吕晓健,高孟潭,陈丹.2010.全球大陆7级浅源大地震强余震震级和空间分布特征[J].地震,30(3):108-122.
- 马茹莹,马震,王培玲,等.2016.青海及邻区地震序列h值震型判定与强余震预测研究[J].地震研究,39(S1):69-75.
- 邵志刚,张浪平.2013.南北地震带北段近期强震趋势研究[J].中国地震,29(1):26-36.
- 苏有锦,李中华,赵小艳,等.2014.全球7级以上地震序列研究[M].昆明:云南大学出版社.
- 陶正如,陶夏新.2021.借助汶川地震损失数据探讨自然灾害等级划分标准[J].灾害学,36(4):31-36.
- 吴果.2018.基于自适应空间光滑模型和三维断层模型的概率地震危险性分析方法研究[D].北京:中国地震局地质研究所.
- 吴开统,焦远碧,王志东.1984.华北地区的晚期强余震特征[J].西北地震学报,6(2):3-43.
- 赵小艳,王光明,张潜,等.2021.2021年云南漾濞MS6.4地震序列特征及强余震判定[J].地震研究,44(3):309-319.
- 中国地震局监测预报司.2007.中国大陆地震序列研究[M].北京:地震出版社.
- 中国地震信息网.2018.地震灾害[EB/OL].(2018-03-01)[2021-04-10].http://www.csi.ac.cn/publish/main/21/1106/index. html.
- Aki K.1965.Maximum likelihood estimate of b in the formula logN=a-bM and its confidence limits[J].Bulletin of Earthquake Research Institute of the University of Tokyo,43:237-238.
- Hamdache M,Pelaez J A,Kijko A,et al.2017.Energetic and spatial characterization of seismicity in the Algeria-Morocco region[J].Natural Hazards,86(S2):73-93.
- Marzocchi W,Sandri L.2003.A review and new insights on the estimation of the b-value and its uncertainty[J].Annals of Geophysics,46(6):1271-1282.
- Mignan A,Woessner J.2012.Estimating the magnitude of completeness for earthquake catalogs[EB/OL].(2017-03-01)[2022-04-10].http://www.corssa.org.
- Okal E A,Romanowicz B A.1994.On the variation of b-values with earthquake size[J].Physics of the Earth and Planetary Interiors,87(1-2):55-76.
- Sandri L,Marzocchi W.2007.A technical note on the bias in the estimation of the b-value and its uncertainty through the Least Squares technique[J].Annals of Geophysics,50(3):329-339.
- Shcherbakov R,Goda K,Ivanian A,et al.2013.Aftershock statistics of major subduction earthquakes[J].Bulletin of the Seismological Society of America,103(6):3222-3234.
- Shcherbakov R,Turcotte D L.2004.A modified form of Bath's law[J].Bulletin of the Seismological Society of America,94(5):1968-1975.
- Wang J H,Chen K C,Leu P L,et al.2015.b-values observations in Taiwan:a review[J].Terrestrial Atmospheric and Oceanic Sciences,26(5):475-492.
- Wiemer S.2001.A software package to analyze seismicity:ZMAP[J].Seismological Research Letters,72(3):373-382.
- Woessner J,Wiemer S.2005.Assessing the quality of earthquake catalogues:Estimating the magnitude of completeness and its uncertainty[J].Bulletin of the Seismological Society of America,95(2):684-698.
![图2 4种组合方法得出的ΔM[TX-]E(a)和CM(b) <br/>Fig.2 ΔM[TX-]E(a)and CM(b)curves resulted from 4 combinations](2022年03期/pic119.jpg)