宝山隧道位于云南省玉溪市峨山县双江街道宝山村,为拟建分离式隧道,右线起止桩号K16+990～K18+630,长度1 640 m; 左线起止桩号ZK17+035～ZK18+657,长度1 622 m。隧道处于高烈度地震带生态脆弱区且洞口位于斜坡地带,坡度约为60°,地形高陡。隧道进口段穿过山体的表层,隧道区洞口及洞身段基本为坡积土层,局部为风化岩,围岩以Ⅳ、Ⅴ级为主,岩土体节理裂隙稍发育,地下水发育。隧道出口覆盖层主要为第四系残坡积角砾、碎石、粉质黏土,均匀性差且厚度不均,岩土体力学性质较差,且洞顶表层土体多处存在裂缝,在天然状态下边坡现状整体存在失稳风险。根据《中国地震动参数区划图》(GB 18306—2015),该区域地震频繁且震级较大。依据地区经验及类似工程经验,综合判定隧道区工程场地类别为Ⅱ类。

由于宝山隧道处于强震区,受地震作用影响,隧道洞口易出现落石灾害、洞门被砸坏、边仰坡滑塌、崩塌、洞门部分堵塞等现象。目前,隧道洞口段二衬局部出现网状开裂,衬砌开裂处发生渗水,严重处出现混凝土剥落,掉块,甚至衬砌垮塌等严重震害类型。隧道现场破损状况如图1所示。

图1 宝山隧道洞口段衬砌震害破损状况
Fig.1 Seismic damage to the lining at the entrance of the Baoshan tunnel

宝山隧道岩体主要为强风化板岩。为了解岩体性质,为数值模拟提供参数,通过现场钻孔取样进行室内力学试验,设置两组实验,每组制备尺寸为50 mm×100 mm的标准圆柱试样各2个,采用英国GDS软岩流变仪及TAW2000电液伺服压力试验机等对试件进行室内试验,测定隧道围岩的相关物理与力学参数。对于试件动弹模量的测定,实验中采用DT-18岩石动弹模量测量仪进行实验,试件为100 mm×100 mm×100 mm的棱柱体。以两组实验所得相应测定值的平均值作为本文中岩体的相关力学参数值。岩体动弹模量计算公式如下:

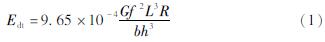
式中:E_dt为动弹模量; G为试件质量; f为试件的自振频率; L、b、h分别表示试件的长、宽、高; R为修正系数,取值1.5。测试结果见表1。

表1 岩体物理力学参数实验结果
Tab.1 Experimental results of the physical and mechanical parameters of rock

考虑隧道工程在数值计算时会产生一定的误差,结合弹性力学中圣维南原理,拟建隧道尺寸应适当放大。杨林德等(2003)和陈国兴等(2010)的研究表明:当计算模型尺寸大于5B(B为隧道开挖宽度)时,隧道模型的边界影响效应较小。为探明震动荷载作用下隧道边坡的稳定性,以确定合理的设防长度,确定隧道模型上部分呈梯形体状,上边界长120 m,下边界长200 m,高130 m,洞口段形成约60°的边坡,隧道数值模型具体细部尺寸如图2所示。该隧道采用Mohr-Coulomb本构模型,Null模型模拟隧道开挖。对于数值模型的边界条件确立,由于隧道最大埋深为134 m,所以并不需要在围岩边界设置等效荷载,选用围岩自重方式对隧道围岩进行加载,模型位移边界固定在水平方向及底部,与现场实际边界条件基本相符。围岩的力学参数值由室内试验测得。

以FLAC3D软件中的动力学分析模块为计算工具对宝山隧道模型进行动力响应分析。对隧道模型赋予室内实验所测得的动力参数,通过zone face apply命令在模型下边界处进行震动荷载的输入,实现震动荷载的加载。在进行隧道地震响应分析之前,先使用FLAC3D软件内置的Dynamic Input Wizard插件对输入的地震波进行基线校正,消除地震波的漂移现象而导致的计算结果失真,震动荷载校正后在模型底部边界输入,震动荷载加载时间为20 s。在数值模型中模拟输入地震波,对比分析隧道模型在不同围岩等级与不同净距工况下的动力响应特征。隧道数值模型动力监测点布置及震动荷载输入方式如图3所示。

图2 宝山隧道模型尺寸
Fig.2 Size of the Baoshan Tunnel model

图3 隧道动力响应监测布置与震动荷载加载示意图
Fig.3 Layout of the dynamic response monitoring of the Tunnel and seismic loading

宝山隧道工程地质复杂、围岩强度弱,隧道开挖后围岩只能保持短暂的稳定,当隧道的初期支护未完全施作时,围岩变形将会超出其所允许的变形范围,产生一定程度的破坏。因此,针对宝山隧道的软弱围岩支护方案拟设计采取超前预支护辅助结构,将超前加固和复合式支护结合起来。洞口段支护结构为超前大管棚预支护结合超前小导管预支护的形式,支护结构参数见表2。隧道洞身段为复合式支护,将锚杆、湿喷砼(采用Φ25钢筋锚杆、锚杆长3.5 m、间距为60 cm,C25混凝土喷29 cm)的初期加固措施和浇筑混凝土(C30钢筋混凝土厚60 cm)的二次支护结合在一起共同加固。支护结构布置如图4所示,其力学性能见表3、图4。

表2 洞口段支护结构参数
Tab.2 Parameters of supporting structures in the opening section

图4 隧道超前预支护(a)和二次支护(b)结构布置示意图(单位:cm)
Fig.4 Schetch of the layout of the Tunnel's pre-support(a)and secondary support(b)structrue

表3 锚杆支护参数
Tab.3 Bolt support parameters

表4 管棚与混凝土支护参数
Tab.4 Parameters of pipe shed and concrete support

为在最大程度上确保计算结果的安全性,同时使得隧道支护结构保留足够的安全储备,本文选取汶川地震波对隧道进行加载,研究截取能量最为集中的波段以速度的方式在FLAC3D有限差分软件中输入。在进行隧道地震响应分析之前,采用FLAC3D软件内置的Dynamic Input Wizard插件对输入的地震波进行基线校正,以此来消除地震波漂移现象的发生而导致计算结果失真的影响。基线校正后汶川地震波的位移时程曲线如图5所示。

图5 汶川地震波位移时程曲线图
Fig.5 Time-history curve of the displacement wave of the Wenchuan eartqhuake

针对高陡边坡小净距隧道洞口段围岩与支护结构动力响应特征进行模拟研究。净距分别选取0.5B、1.5B两种相对位置,由于工程中岩体主要以Ⅳ、Ⅴ级围岩为主,随着净距的扩大,左右双线隧道所处围岩级别存在一定差异,故数值模拟中围岩级分别选取Ⅳ、Ⅴ级进行分析,工况信息见表5。

表5 数值模拟工况
Tab.5 Numerical simulation conditions

通过数值模拟计算得出各工况条件下的不同围岩监测断面峰值位移变化规律,如图6a所示。由图6a-1可知,当隧道洞口段穿越Ⅳ级围岩时,双洞净距为0.5B时隧道监测断面各点的峰值位移随隧道进深的增加而呈现下降趋势,在下降的过程中围岩峰值位移呈现出一个较明显的临界点,该临界点以距洞口距离为55 m(4.2B)为标志。临界点前段围岩峰值位移最高达52.0 cm,位移下降率仅为0.073%; 临界点后段围岩径向峰值位移下降率增大,达到0.6%,此时围岩位移为29 cm并开始趋于缓和。对比分析图6a-1、a-2可以看出,同一净距条件下,Ⅴ级围岩峰值位移大于Ⅳ级围岩,最大值为62.5 cm,较Ⅳ级围岩增大20.2%,位移峰值下降率增大位置距洞口74.5 m(5.7B),较Ⅳ级围岩延后19.5 m,且临界值所出现的位置相对于推迟。

由工况1与工况2可知,隧道洞口段抗震设防长度很大程度上取决于围岩岩体性质,且与岩体等级呈负相关关系。同一净距条件下,围岩等级越高,岩体条件越好。隧道受震动荷载的扰动效应越弱,洞口段相应抗震设防长度要求也越低。在此基础上探明了对应围岩等级下的隧道洞口段抗震合理设防长度。为进一步探究除岩体性质外的隧道净距对隧道洞口段抗震性的影响规律,模拟计算中改变双线隧道的净距为1.5B,采用围岩等级为Ⅴ级,计算得出隧道在汶川波作用下径向位移峰值响应规律如图6a-3所示。

对比分析图6a-2与图6a-3可得:在同一围岩等级条件下,不同净距隧道各关键点的峰值位移变化规律基本相似,只是数值不同。当隧道净距扩大到1.5B时,位移下降率升高临界点位于距洞口39 m(3.0B)处,临界点前段位移峰值最大达到37.4 cm,发生在拱顶位置处,位移峰值下降率约为0.188%; 临界点后位移峰值下降率为0.8%,围岩趋于稳定。

图6 隧道监测断面峰值位移变化规律(a)和衬砌结构轴力纵向响应规律(b)
Fig.6 Variation law of the peak displacement of the Tunnel's monitoring section(a)and the longitudinal response law of the lining axial force(b)

分析图7a结果可知:隧道在震动荷载影响的最不利工况下(工况2),衬砌结构位移的响应值突出区域主要分布于距洞口75 m(5.7B)内,在较安全工况下(工况1、3),衬砌结构位移的响应值突出区域主要分布于距洞口39 m(3.0B)与55 m(4.2B)以内。因此,建议取75 m(5.7B)作为隧道洞口合理设防长度。

从隧道监测断面峰值位移沿隧道进深的变化规律确定出一个合理的隧道抗震设防范围,采用隧道衬砌结构轴力峰值响应对上述结果进行验证,隧道衬砌结构轴力纵向响应计算结果如图7b所示。

从图7b可以看出,沿隧道进深方向,不同工况下衬砌结构的动力响应逐渐减弱并趋于稳定。对于工况1(图6b-1),衬砌结构最大轴力位于右拱脚处,为1 172 kN。随着隧道进深的增加,隧道受震动荷载的作用效应逐渐减弱,在距洞口62 m(4.7B)处衬砌轴力开始趋于稳定,其值为623 kN,比洞口段衬砌结构轴力减少47.2%。对于工况2(6b-2)衬砌结构轴力,其最大值位于左拱脚处,洞口段峰值达1 320 kN,比Ⅳ级围岩时增大10%,轴力下降率减小的临界点出现在距洞口72.4 m(5.5B)位置,较Ⅳ级围岩条件下延后了12.4 m,此后轴力下降率逐渐减小并趋于稳定。对比分析工况2、3(6b-2、b-3)可知,在水平纵向地震动作用下,当隧道净距增大后,隧道受震动荷载作用的扰动效应降低,隧道衬砌结构轴力下降率减小的临界点向洞口靠近,为距洞口39 m(3B),且整体数值约减小23%。

综合震动荷载作用下衬砌结构轴力峰值的计算结果可知:隧道在震动荷载影响的最不利工况下(工况2),衬砌结构轴力的响应值突出区域主要分布于距洞口72.4 m(5.5B)内,在较安全工况下(工况1、3),衬砌结构轴力的响应值突出区域主要分布于距洞口39 m(3B)与62 m(4.7B)以内。因此,基于衬砌安全使用的隧道洞口合理设防长度建议值应取为72.4 m(5.5B)。

由上述位移与轴力计算结果可知,不同隧道净距与围岩级别对隧道抗震性影响差异较大,工况2下隧道所需设防长度为上限。为精确确定不同因素相互影响下隧道抗震合理设防长度的具体值,针对工况1与工况3,对其震动荷载作用下衬砌的剪力、弯矩及主应力进行对比,确定最终隧道合理抗震设防长度下限值,计算结果如图7所示。

由图7可知:沿隧道进深方向,两种工况下,衬砌产生的剪力、弯矩及最大主应力的变化基本一致。在工况1下,虽然岩体质量较好,但隧道净距较小,剪力趋于稳定的断面距洞口间距为65 m(5B)。而工况3相比于工况1,围岩级别降低,但隧道双线净距增大至1.5B,此时剪力趋于稳定的断面距洞口间距为39 m(3B),隧道受震动荷载作用的动力响应范围大大缩小。而针对衬砌所产生的弯矩与最大主应力,在工况1下,弯矩与主应力最大值分别为128 kN·m、1 100 kPa,而趋于稳定时分别为60 kN·m、575 kPa,趋于稳定的断面距洞口距离分别为6.0B、5.5B。工况3下,弯矩与主应力其最大值分别为92 kN·m、910 kPa,而趋于稳定时分别为47 kN·m、480 kPa,趋于稳定时断面距洞口间距分别为3.4B、3.8B。

由上述可知,在围岩等级与隧道净距这两个影响因素中,隧道净距对隧道抗震性的影响程度大于隧道围岩等级。为探究不同净距的影响效应,选取8组同一围岩等级、不同净距隧道进行震动模拟,模拟计算结果如图8所示。

图7 断面监测点剪力(a)、弯矩(b)和主应力(c)纵向变化规律
Fig.7 Longitudinal variation law of shear force(a),bending moment(b)and principal stress(c)at cross-section monitoring points

图8 不同净距隧道中夹岩柱的塑性区分布
Fig.8 Distribution of the plastic zone of rock pillars in tunnels with different clear distances

从图8中可以看出,当隧道净距较小时,双线隧道围岩塑性区产生交会,使得隧道在震动荷载下的稳定性大大降低。随着隧道净距的扩大,双线隧道中夹岩柱厚度增大,左右双线隧道围岩塑性区交会部分逐渐减小,在1.2B的时候不再产生交会,围岩发挥一定承载能力使得隧道抗震性能有所提升,隧道所需抗震设防长度相应缩短。

综上认为:在Ⅴ级围岩条件下,可分别取6.0B、3.5B作为0.5B与1.5B小净距隧道的洞口抗震合理设防长度; Ⅳ级围岩条件下,取5.7B作为0.5B小净距隧道的洞口抗震合理设防长度。宝山隧道净距13 m,隧道穿越围岩主要为Ⅳ、Ⅴ级围岩。基于以上分析,为确保隧道在震动荷载作用下维持稳定且具有一定安全储备,宝山隧道在最不利条件下洞口段合理设防长度应取为6.0B(78 m)。