基金项目:国家自然科学基金项目(51378169); 河北省高等学校科学技术研究重点项目(ZD20161470).
第一作者简介:申彦利(1977-),教授,博士后,主要从事结构抗震方面的研究.E-mail:shenyanli@hebeu.edu.cn.
(1.河北工程大学 土木工程学院,河北 邯郸 056038; 2.河北省装配式结构技术创新中心,河北 邯郸 056038)
(1.School of Civil Engineering,Hebei University of Engineering,Handan 056038,Hebei,China)(2.Hebei Provincel Prefabricated Structure Technology Innovation Center,Handan 056038,Hebei,China)
wind turbine tower; incremental dynamic analysis; higher order modes; structural demand; seismic vulnerability
DOI: 10.20015/j.cnki.ISSN1000-0666.2024.0050
风电是重要的可再生能源,2022年全球新增风电并网容量达77.6 GW,风电总装机容量达906 GW,比2021年增长9%(Global Wind Energy Council,2023)。我国风电产业正处在高速发展阶段,总装机容量和新增装机容量均处于世界前列。值得注意的是,我国虽然是地震多发国,但在高烈度地区,对风电设备的建设也有着相当大的需求,因此,风电塔筒的地震风险不容忽视。风电塔筒结构上部机舱及叶片的重量比较大,在地震作用下塔筒可能会发生过大变形,经济损失不可估量,因此,研究塔筒的地震响应并开展地震易损性分析具有重要意义。
近年来,各种类型风电塔筒的地震易损性问题开始受到国内外学者的关注。Patil等(2016)针对一座风机钢塔筒结构进行了地震易损性分析,指出了整体屈曲、基础倾覆、首次屈服、永久变形4种极限状态,其中基础倾覆最为关键且近场地震更容易引起风机的破坏。曹雨奇等(2018)以水平位移角作为损伤指标,对体外预应力混凝土塔筒进行地震易损性分析,分析了该类型塔筒在Ⅶ度多遇地震条件下的损伤情况。王浩(2020)和梁睿(2019)分别对钢-混凝土混合塔筒及混凝土塔筒进行振动损伤机理研究,发现在地震动作用下,塔筒的损伤范围从塔筒底部逐渐向上延伸,损伤程度最大的区域集中在塔筒底部与基础相接处的位置。戴靠山等(2018)开展了某风力发电塔架缩尺模型振动台试验,指出塔筒在地震作用下会产生高阶振型效应。
结构地震易损性分析的关键在于地震动强度参数的选择,目前人们对风电塔结构地震易损性的研究中常选用谱加速度Sa、峰值加速度PGA。叶列平(2009)的研究表明,Sa不太适用于多自由度结构的抗震分析,而PGA仅适用于短周期结构,无法较好地反映中长周期结构的地震响应。风电塔筒较为细长,是典型的中长周期结构,为使模拟结果更加精准,本文采用张超和申彦利(2017)提出的考虑了结构高阶振型效应的复合参数IM1I&2E作为地震动强度参数,运用OpenSees分析软件建立钢-混凝土混合风电塔筒二维数值模型,基于推覆分析确定各损伤状态的限值,以截面曲率作为结构需求参数,选取20条真实的地震动记录进行塔筒的增量动力分析,建立塔筒的地震易损性曲线并对其进行评估,以期为钢-混凝土混合塔筒的抗震设计以及抗震加固提供参考。
为研究地震作用下钢-混凝土混合风电塔筒的抗震性能,本文选取建于Ⅶ度设防区的某钢-混凝土混合风电塔筒(图1)为研究对象。风电塔所在地的设计基本地震加速度为0.15 g,设计地震分组为第三组,场地类别为Ⅱ类,特征周期为0.45 s。该塔总高度为121.5 m,下部为80 m的混凝土塔筒,上部为40 m的钢筒,两者中间为高度1.5 m的钢混过渡段,塔筒上方机舱及叶片的总质量为215 t。混凝土筒段底部直径为6 m,顶部直径为4 m,钢筒段底部直径为3.5 m,顶部直径为2.6 m,筒身壁厚沿高度均匀变化,各筒段截面形式为均匀渐变形式。
钢-混凝土混合塔筒的计算使用OpenSees进行建模,建模中将风电塔简化为底部固结的单悬臂结构,塔筒上部机舱及叶片的质量简化为集中质量施加于塔筒顶部,筒身的分布质量等效为节点质量。风电塔筒尺寸示意图及计算简图如图2所示。
图2 风电塔筒尺寸示意图(a)及计算简图(b)
Fig.2 Dimensions of the wind turbine tower(a) and the tower's sketch for calculation(b)
众多学者在桥梁高墩的研究中使用纤维梁柱单元进行建模。曹雨奇等(2018)在体外预应力混凝土风力发电塔的研究中指出纤维梁柱单元建模技术可在相似结构的分析中使用。为确保模型的准确性,本文根据前人的建模理论,使用基于位移的纤维梁柱单元模拟筒身,沿高度方向每5 m划分一个单元,其中钢混过渡段单独设置一个单元,其长度为1.5 m,每个单元设置两个积分截面; 单元截面使用纤维截面进行模拟,混凝土筒段沿圆周方向划分120个纤维,径向划分6个,共计720个纤维; 钢筒段和过渡段沿圆周方向划分120个纤维,径向划分1个,共计120个纤维; 混凝土筒段的纵向钢筋根据内外圈钢筋的数目、截面面积以及位置建立相应的纤维,如图3所示。
混凝土段纤维截面根据约束条件分为保护层混凝土和核心区混凝土,其材料强度等级为C60,选用OpenSees材料库中的Concrete 02材料进行模拟,其本构参数选择Kent-Scott-Park模型(Scott et al,1982)计算,该模型考虑了箍筋约束对混凝土强度的增强作用。混凝土筒段钢筋的强度等级为HRB400,钢筒段钢材为Q345钢,两者用材料库中的Steel 02材料进行模拟,本构参数选用Giuffre-Menegotto-Piano模型(Menegotto,Pinto,1973)进行计算。两种模型的本构关系如图4a、b所示,ε0为混凝土峰值应变,εu为混凝土极限压应变,fc为混凝土抗压强度,fcu为极限抗压强度,Ec为混凝土弹性模量,Etc为受拉软化刚度,λ为卸载刚度比,ft为抗拉强度,fy为屈服强度,E为弹性模量,Ep为屈服后的模量,各参数具体值见表1、图2。
图4 混凝土(a)和钢筋(b)本构关系
Fig.4 The concrete constitutive relation(a)and the reinforcement constitutive relation(b)
结构的损伤指标是用来定义结构损伤状态的物理量,它代表着结构的抗震能力。在地震易损性研究中常用的损伤指标有位移指标、曲率指标等。多数桥梁高墩的研究表明(梁智垚,2007; 肖明洋,2013; 赵志宏,2021; 石岩等,2022),高墩在地震作用下会产生高阶振型效应,此时墩顶位移与控制截面曲率不再满足对应关系,如果采用位移损伤指标进行地震易损性分析则会有较大误差,此时结构的损伤状态不能通过位移指标表现。而风电塔筒与高墩类似,具有周期长、柔度大的特性,位移指标不能充分体现塔筒的损伤状态。从材料角度来看,材料应变可以充分反应结构的弹塑性损伤状态,但其计算量庞大,需要分析结构中每根纤维的响应; 为简化计算,本文选用可以体现应变关系的截面曲率作为结构损伤指标。相关研究(王浩,2020; 丁立勇,2018)表明,在地震作用下塔筒基底位置的损伤程度最大,因此,本文选取塔筒底截面作为控制截面进行地震易损性分析。
对模型进行推覆分析(Pushover分析)得到基底剪力与顶点位移曲线如图5a所示。Pushover分析采用顶点位移加载模式,当加载至倾覆时,分析塔筒的变形和应力应变可知,筒身底部位置处变形最为显著,钢筒段及钢混过渡段不会发生屈曲破坏,由此可知,塔筒的脆弱部位在底部。根据基底剪力与顶点位移曲线的特性,提取出4个性能点分别对应4种极限状态LSi,同时参考《建(构)筑物地震破坏等级划分》(GB/T 24335—2009)中的定义将塔筒的损伤状态划分为完好、轻微损伤、中等损伤、严重损伤、完全破坏5种损伤状态,各极限状态对应的曲率值见图5b,各损伤状态描述见表3。
图5 基底剪力与顶点位移(a)和曲率与顶点位移(b)曲线
Fig.5 Base shear vs vertex displacement(a)and curvature vs vertex displacement(b)
对于增量动力分析而言,地震波的选择对模拟结果有较大影响。为使模拟结果更加精准,本文根据地震波的峰值、频谱特性、持时三种特性,结合《建筑抗震设计规范》(GB 50010—2010),从美国太平洋地震工程研究中心(PEER)强震数据库中选取80条地震波记录,根据各主要振型周期内加速度值相差不超过20%的原则(谢丰蔚,2015),从中挑选出20条与设计反应谱相匹配的地震波记录(表4)做谱分析,其反应谱曲线如图6所示。
目前结构地震易损性分析中大多采用地面峰值加速度PGA和谱加速度Sa,其中PGA的应用最为广泛。叶列平等(2009)的研究指出,在中长周期范围,结构地震响应与PGA的相关程度较小,PGA无法较好地模拟中长周期结构的地震响应,
而Sa又不太适合在多自由度结构地震响应分析中使用。张超和申彦利(2017)提出了一种考虑结构前两阶振型影响的复合地震动强度参数IM1I&2E,其表达式为:
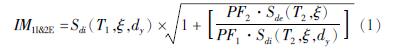
式中:PF1为第一阶振型影响参与系数; PF2为第 二阶振型影响参与系数; Sdi(T1,ξ,dy)为第一振型所对应的非弹性位移谱值; Sde(T2,ξ)为第二振型所对应的弹性位移谱值。该强度参数综合考虑结构第一振型所对应的非弹性移谱值Sdi(T1,ξ,dy)和第二振型所对应的弹性位移谱值Sde(T2,ξ),对中长周期结构的抗震性能评估具有良好的适用性,能更加准确地评估塔筒的抗震性能。因此,本文选取复合地震动强度参数IM1I&2E作为地震动强度参数进行地震易损性分析。对模型进行模态分析并结合前文的Pushover分析结果得到其动力特性参数(表5)。
对选取的20条地震动进行调幅处理,调幅后的峰值地面加速度分别为0.05 g,0.1 g,0.15 g,0.2 g,…,1.0 g,调幅步长为0.05 g。利用调幅后得到的400条地震动记录进行增量动力分析(IDA),地震动采用基底一致激励方式沿X方向单向输入,记录结构在不同地震动作用下控制截面的响应。以地震动强度参数IM1I&2E为横坐标,以曲率为纵坐标,得到IDA曲线如图7所示。
图7 20条地震动作用下塔筒IM1I&2E-曲率IDA曲线
Fig.7 IM1I&2E-curvature IDA curves of the tower when inputting 20 ground motions
将增量动力分析得到地震动强度参数与截面曲率形成的400个离散数据点在对数坐标系中表示,如图8所示,并对其进行二次多项式回归拟合,建立控制截面曲率与复合地震动强度参数间的函数关系式:
ln(φ)=0.168[ln(IM1I&2E)]2+1.84(IM1I&2E)-7.61 (2)
结构的地震易损性可以描述为结构或构件在地震作用下地震需求超越抗震能力的概率,是一种基于概率的结构抗震性能评估方法,可表示为:
F(v)=Pf[Ls|IM=y]=P[C≤D|IM=y] (3)
式中:Ls为极限状态; C代表结构能力; D代表结构需求。通常认为C和D是两个独立的随机变量,二者均服从对数正态分布(Choi et al,2003),则上式可以转化为:

式中:Ф(*)表示标准正态分布函数; Sd表示结构需求均值、Sc表示结构能力均值; βd为结构需求对数标准差; βc为结构能力对数标准差; 其中βd根据地震需求模型求得,βc根据Wen等(2003)的研究取值为0.3。将由IDA方法得出的地震动强度与结构需求之间的关系式代入式(4)中即可得塔筒在不同地震动强度下的损伤超越概率:
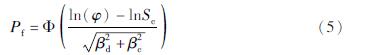
由塔筒地震易损性曲线(图9)可知,各损伤状态的超越概率与复合地震动强度参数IM1I&2E呈正相关性,轻微损伤曲线与中等损伤曲线在一定范围内迅速上升,而严重损伤状态曲线和完全破坏状态曲线较为平缓,说明塔筒有较好的抗震能力。IM1I&2E相同时,塔筒出现发生轻微损伤、中等损伤、严重损伤、完全破坏的概率逐步降低。当IM1I&2E<0.1时,塔筒各损伤状态的概率基本为零; 当0.2<IM1I&2E<0.5时,塔筒发生中等损伤的概率明显上升。
该风电塔所在区域为Ⅶ度设防区(0.15 g),由式(1)可计算出其地震动强度参数IM1I&2E值为0.25,由图9可知塔筒发生轻微损伤的概率为89%,发生中等损伤的概率为11%,其它损伤状态概率基本为0; 结合表3中的描述可知结构几乎处于弹性工作状态,发生中等损伤的概率比较低,即使发生轻微损伤,其基本使用功能也不受影响,处于稍加修理可继续使用状态,满足“中震可修”的要求。
在Ⅶ度罕遇地震下(0.22 g),IM1I&2E=0.37,塔筒发生轻微损伤和中等损伤的概率分别为99.6%、58.8%,其它损伤状态概率基本为0,发生倒塌的可能性很小,满足“大震不倒”的要求,由此可以认为该风电塔筒可以满足Ⅶ度抗震设防区的抗震要求。
在Ⅷ度罕遇地震下(0.4 g),IM1I&2E=0.68,塔筒发生轻微损伤、中等损伤、严重损伤、完全破坏的概率分别为100%、99.7%、9.78%、0,在此条件下,塔筒会发生一定程度的损伤,但倒塌的可能性很低,需要综合考虑经济成本及经济效益合理选择抗震设计。
本文基于弹塑性纤维梁柱单元理论建立了某钢-混凝土风电塔筒二维数值模型,以复合参数IM1I&2E作为地震动强度指标,以截面曲率作为损伤指标,用增量动力分析方法建立了塔筒在20条地震波作用下的易损性曲线,根据易损性分析结果得出如下结论:
(1)塔筒的损伤程度与地震动强度参数呈正相关态势,在相同地震动强度参数下,塔筒发生轻微损伤、中等损伤、严重损伤和完全破坏的概率依次减小。
(2)该风电塔所在区域地震动强度参数IM1I&2E值为0.25,塔筒轻微损伤的概率为89%,发生中等损伤的概率为11%,其它损伤状态概率基本为0,可以满足该地区抗震设防要求。
(3)在Ⅷ度罕遇地震(0.4 g)作用下塔筒会发生一定程度的损伤,对于高烈度地区的风电塔,建议综合考虑经济成本及经济效益,合理选择抗震设计。