基金项目:国家自然科学基金(42174111); 北京市自然科学基金(8222033); 上海佘山地球物理国家野外科学观测研究站开放基金项目(SSOP202203).
第一作者简介:李孟洋(1995-),博士研究生在读,主要从事地震数值模拟、地震层析成像方面的研究.E-mail:limengyang22@mails.ucas.ac.cn.
通信作者简介:刘少林(1988-),研究员,主要从事地震波正反演研究.E-mail:shaolinliu88@163.com.
(1.中国科学院大学 地球与行星科学学院,北京 100049; 2.应急管理部国家自然灾害防治研究院,北京 100085; 3.清华大学 数学科学系,北京 100084; 4.中国地质大学 地球物理与空间信息学院,武汉 430074)
(1.College of Earth and Planetary Sciences,University of Chinese Academy of Sciences,Beijing 100049,China)(2.National Institute of Natural Hazards,Ministry of Emergency Management of China,Beijing 100085,China)(3.Department of Mathematical Sciences,Tsinghua University,Beijing 100084,China)(4.Institute of Geophysics and Geomatics,China University of Geosciences,Wuhan 430074,Hubei,China)
the spectral element method; seismic wave function; numerical simulation; δ function
DOI: 10.20015/j.cnki.ISSN1000-0666.2025.0042
地震成像通过拟合地震波观测数据和合成数据(理论计算数据)反演地球内部介质参数,是研究地球内部结构的主要方法之一(Lei et al,2023; Lin et al,2023)。目前基于地震波形的成像方法,如逆时偏移成像(Feng,Schuster,2017; Cho,Gibson,2019)、地震波形层析成像(李冰非等,2019)等,已被广泛应用于地球浅深部结构成像(刘玉柱等,2019; 王光文等,2023)。在开展地震波形成像研究时,地震波数值模拟是其中的关键步骤,目前地震波数值模拟方法主要为有限差分方法(Finite-difference Method,FDM)(Chen et al,2011; Lyu et al,2020)、有限元法(Finite-element Method,FEM)(Liu et al,2014; Yao et al,2018)和谱元法(Spectral-element Method,SEM)(Tromp et al,2008; Mazzieri et al,2013)等。FDM因具有数值计算效率高、实现相对简单的优点而被广泛应用于地震波数值模拟中,但该方法通常使用规则矩形网格模拟地震波传播,而矩形网格模型难以拟合复杂界面。另外,在模型自由地表边界处,难以通过FDM施加自由地表边界条件。因此,当研究区地形较为复杂时,使用该方法难以精确模拟地震波传播(杨尚倍等,2018; Yi et al,2019)。FEM具有网格灵活性,可采用非规则网格拟合自由地表,并可自动满足自由地表边界条件,然而FEM计算效率较低(Bielak et al,2005)。SEM是一种模拟效率较高的方法,该方法具有网格灵活性,并具有自动满足自由地表边界条件的优点,能在复杂模型中精确模拟地震波传播。因此,SEM作为一种高精度地震波模拟方法而逐渐被应用于地震成像中(Tromp et al,2005; Tape et al,2010; Tong et al,2014)。
利用数值模拟地震波传播时,需要对地震波运动方程进行离散化处理。将震源近似为点源时,或将有限断层破裂面分解为若干个点源时(Shen et al,2022),地震波运动方程中震源项包含δ函数(Lay,1992)。在数值模拟地震波传播中,SEM可使用插值多项式离散震源项,由于这种震源处理方式较为简单,国内外大多数学者使用该方法处理震源项(Komatitsch,Tromp,1999; 刘少林等,2021; 孟雪莉等,2022)。震源项的离散形式也可通过直接离散δ函数的方法得到,但由于δ函数是奇异函数,难以直接通过数值近似方法离散,若离散方式不合理,将会造成模拟地震波场产生虚假波动(Jung,2009; Zang et al,2021)。
为了离散δ函数,本文借鉴FDM处理震源项的思想,通过引入伪δ函数得到δ函数离散形式(Herrmann,1979; Jung,2009),可得到第一类δ函数离散形式。考虑到离散点采样的波数响应函数在波数域为有界函数的特征,在波数域设计一个窗函数,然后对该窗函数进行傅立叶逆变换,得到了第二类δ函数离散形式。将2类δ函数离散形式应用于SEM中,并模拟点源激发的地震波传播。为了检验SEM模拟地震波传播时利用δ函数离散形式处理点源的可行性,最后开展了多组数值算例,分析了震源项处理方式对不同类型地震点源的处理能力。
为论述简便,本文以二维情况为例,简要介绍了SEM求解弹性波动方程的基本原理。在二维非均匀各向同性介质中,弹性波运动方程可表示为:

式中:ρ为介质密度; u为位移矢量; ü为位移对时间的二阶导数; 为梯度算子; T为应力张量; c为弹性张量; 假设震源为点源,震源项f表达式为:

或
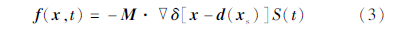
式中:f(x,t)为震源函数; Is为震源分量向量; M为地震矩张量; 为空间梯度算子; δ(x)为空间δ函数; d(xs)为震源位置; S(t)为震源时间函数。
式(1)为弹性波运动方程的强形式,利用变分原理可以得到式(1)的弱形式。首先将式(1)两端同时乘以测试向量w可得:
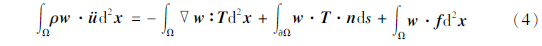
式中:Ω为计算区域; n为计算区域单位法向量;Ω为计算区域边界。在地球自由地表处满足边界条件T·n=0(即地表法向应力为0),所以式(4)可简化为:
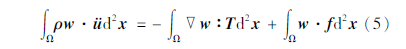
式(5)即为弹性波运动方程的弱形式。相对于式(1)而言,式(5)具有自动满足自由地表边界条件的优点。如果使用SEM数值求解弹性波运动方程,首先需要将计算区域Ω离散为Ne个不重叠的四边形单元Ωe(二维情况下),为了降低计算复杂度,通常将物理域单元Ωe转换到参考域单元Ω'e,然后在参考域求解式(5)。Ωe与Ω'[KG-*4]e的数值映射关系为(Komatitsch,Tromp,1999):
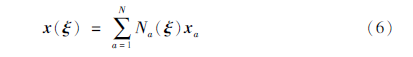
式中: x=(x, z)为物理域中的坐标; ξ=(ξ1, ξ2)为参考单元上的坐标, 且-1≤ξ1≤1、-1≤ξ2≤1; [KG-1]N为单元节点数; Na(ξ)为关于第a个插值节点的形函数, 由Legendre多项式构成; xa为参考单元控制点在物理域中的坐标。某个单元e内的函数值可以通过Lagrange多项式插值表示:
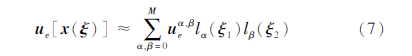
式中:lα(ξ1)和lβ(ξ1)为Lagrange插值基函数; M为插值阶数。将式(7)带入式(5)中并消去测试向量w可得到式(4)的离散形式(Komatitsch,Tromp,1999; 刘少林等,2021):
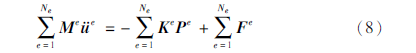
式中:Me为单元质量矩阵; Ke为单元刚度矩阵; Pe为与单元介质参数、雅克比矩阵和坐标转换因子有关的向量; Fe为单元震源项离散形式。矩阵和向量的具体形式参见附录A。
根据式(2)和式(4)可得弹性波运动方程的震源项表达式为:
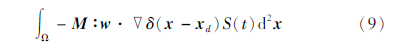
本文使用3种方法处理δ函数:第一种方法使用空间平滑的伪δ函数直接得到其离散形式,称之为第一类离散形式; 第二种方法通过对窗函数进行傅立叶逆变换得到δ函数离散形式,称之为第二类离散形式; 第三种方法通过插值形函数得到震源项的离散形式,该方法的详细介绍参见附录A。下面详细介绍第一和第二种震源处理方法。
为了更好地使用网格节点离散δ函数,选用的伪δ函数应具有空间光滑特征,因此本文选用Herrmann(1979)提出的伪δ函数,称之为第一类离散形式,δ~函数为光滑函数,其图像如图1所示,且函数表达形式较简单,其一维表达式为:
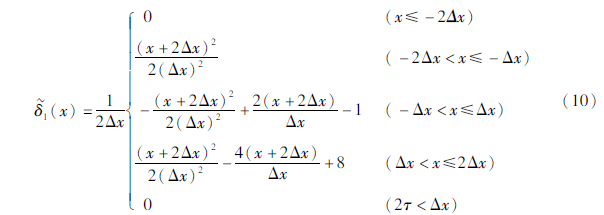
式中:Δx为网格间距。
图1 第一类δ函数离散形式(δ~1)
Fig.1 The first type of discrete form of δ function(δ~1)
δ函数的理论波数响应为1,即在所有波数范围具有相同的振幅。在近似理论δ函数时,近似δ函数的波数响应特征应与理论δ函数相近。间隔为Δx的离散点采样极限频率为1/(2Δx),使用间隔为x的离散点近似δ函数时,应尽量满足该函数的波数响应在0~1/[KG0](2Δx)范围内接近于1。因此,在波数域设计一个窗函数,然后对该窗函数进行傅立叶逆变换得到其波数响应,也可得到δ函数离散形式,称之为第二类离散形式。为了检验该方法得到的δ函数离散形式在地震波模拟时处理地震点源的有效性,首先本文在波数域确定了采样点,采样点在波数0~1/[KG0](2Δx)范围内的波数谱幅值接近1。然后对采样点进行插值平滑处理得到一组平滑的波数谱函数H(k)(图2a),通过傅立叶逆变换求取H(k)的单位脉冲响应即可得到δ函数第二类离散形式(δ~2)(图2b)。由于δ2函数具体表达式较难给出,因此本文在表1中列出了该离散函数的离散数值。
使用δ函数离散形式具有2个优点:①函数空间分布较为平滑(图1、图2b),可以显著地减小由于震源函数空间不连续引起的地震波虚假振动(Jung,2009; Zang et al,2021); ②离散δ函数具有普适性,可用于FDM、FEM以及SEM中的点源近似问题。以第一类δ函数离散形式(δ~1)为例,二维情况下δ函数的近似表达式为:
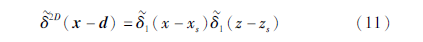
式中:d(xs,zs)为震源位置。将式(11)和式(7)代入到式(9)可得:
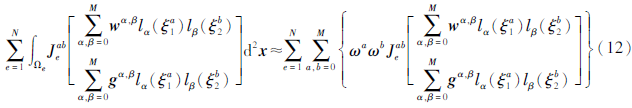
表1 第二类δ函数离散数值(δ~2)
Tab.1 The second type of discrete values of δ function(δ~2)
图2 波数谱函数H(k)(a)以及第二类δ函数离散形式(δ~2)(b)
Fig.2 The wave number spectrum function H(k)(a) and the second type of discrete form of δ function(δ~2)(b)
式中:g为地震矩张量M和δ~1函数的组合变量:
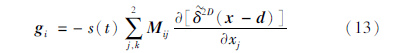
式(12)和(13)即为第一类δ函数离散形式的震源项表达式。
在数值模拟中,本文称使用δ函数第一类离散形式处理震源的地震波模拟方法为M1,为了对比需要,称使用δ函数第二类离散形式处理震源的地震波模拟方法为M2,称使用插值形函数处理震源的地震波模拟方法为M3。M3方法是SEM中较为常用的一种震源处理方法(Komatitsch,Tromp,1999; 刘少林等,2021; 孟雪莉等,2022),但M1和M2方法使用较少。因此,在SEM中使用M1和M2方法处理震源的可行性仍需检验。
为了研究在SEM地震波模拟中使用δ函数离散形式处理震源的可行性,本文首先开展了3组数值算例测试。第一组算例测试了使用δ函数离散形式处理单极震源(Aki,Richards,2002; Hicks,2002)的有效性。第二组算例测试了使用δ函数离散形式处理地震矩张量震源的有效性。这两组算例中离散模型由正方形网格构成。第三组算例测试了离散模型由非规则网格构成时,使用δ函数离散形式处理震源的可行性,因此该算例中使用的离散模型由非规则网格构成。为了测试δ函数离散形式在FDM地震波模拟中处理震源的可行性,本文开展了第四组数值算例测试。
4组算例中震源时间函数S(t)为Ricker子波,其主频为20 Hz。模型介质P波速度为2 000 m/s,S波速度为1 250 m/s,密度为2 000 kg/m3,震源参数和模型参数如图3所示。数值模拟地震波时,最短波长的网格点数应大于4(刘璐等,2013),因此本节算例中SEM离散单元边长设置为20 m左右,空间采用6阶插值(最短波长网格点数约为16)。时间离散步长设置为0.2 ms,地震波模拟时长为0.6 s。
本文首先考虑一种简单情况,震源为单极震源,表达式为f=δ(x-d)S(t)Is,单极震源激发的地震波在无限半空间介质的解析解可通过Cagniard de Hoop方法计算(De Hoop,1959)。模拟数值解通过与解析解比较,可定量分析模拟数值解的精度。
为分析在SEM模拟中使用M1、M2和M3方法处理震源的有效性,本节首先开展了单极震源(脉冲震源)数值算例测试。该算例模拟了一个垂直集中力源(Is=[0,1]T)激发的地震波在介质中的传播。为了防止地震波在人工边界处产生虚假反射,除自由地表边界外(模型上边界)的其他边界使用PML吸收边界吸收虚假反射(Liu et al,2014)。
使用SEM模拟地震波得到合成波形,由模拟结果减去解析解后除以解析解振幅最大值得到相对误差,如图4所示。图4a为接收器R1、R2记录的SEM合成波形与解析波形的水平和垂直分量。从图中可以看出,M1、M2和M3方法模拟得到的合成波形与解析波形具有较好的一致性。为了进一步对比3种方法的模拟结果,计算接收器R1、R2记录的SEM合成波形相对于解析解的相对误差。从图4b中可以看出,M2和M3模拟结果具有较高的精度(最大波形误差小于5%),但M1模拟结果精度相对较低(最大波形误差为8%左右),说明在使用SEM开展地震波模拟时,使用M2和M3方法处理震源可得到精度较高的模拟结果,且模拟得到的波形不需要进行归一化处理即可与解析解较好地匹配。
为了测试M2方法能否精确模拟使用地震矩张量震源(点源)激发的地震波场,本组算例选用了2个不同的地震矩张量,模拟了地震矩张量震源激发的地震波场,为了对比需要,选用M3方法模拟结果作为参考解。本组测试中使用2种类型地震矩张量震源(S1和S2),其地震矩张量分别为:

和

模拟地震波结果如图5~8所示。其中,震源S1为垂直集中力源,震源S2为爆炸源。模型参数如图3所示。图5展示了垂直集中力源(S1)的地震波场快照,从图中可看到清晰的P波和S波震相。从震源S1激发的地震波场在接收器R1和R2处的合成波形(图6a)可看出,M2方法模拟得到的合成波形与参考解(M3方法模拟结果)具有较好的一致性,且波形精度较高(相对误差最大值约为4%)(图6b)。图7展示了爆炸源(S2)的地震波场快照,波场快照显示震源S2只激发出P波震相,M2方法模拟波场与参考波场的空间分布(M3方法模拟结果)具有高度相似性。从震源S2激发的地震波场在接收器R1和R2处合成波形(图8)可看出,M2方法的合成波形与参考解(M3方法模拟结果)具有较好的一致性,且波形模拟精度较高,相对误差较小(相对误差最大值约为4%)[KG0.15mm。](图8b)。因此,地震矩张量震源(点源)激发的地震波场,使用M2方法可得到精度较高的模拟结果。
图4 接收器R1、R2记录的SEM合成波形与解析波形对比(a)以及两者的相对误差(b)
Fig.4 The SEM synthetic waveforms and analytical waveforms of Receiver 1 and Receiver 2(a),and their relative errors(b)
为了测试当震源位于非规则网格时使用M2方法模拟地震波场的可行性,本组算例构建了如图9所示的非规则网格模型,实际单元尺寸约为20 m,为了直观地展示该模型,图中单元尺寸放大2倍, 图中也展示了模型参数。本组算例震源类型为S1,使用M2方法进行了地震波模拟,为了对比需要,选用M3方法模拟结果作为参考解。
图6 震源为S1时,接收器R1、R2的SEM合成波形与参考波形(a)以及两者的相对误差(b)
Fig.6 The SEM synthetic and analytical waveforms of the Source 1-excited waveforms received by Receiver 1 and Receiver 2(a)and their relative errors(b)
图7 t=0.4 s时,使用M2、M3方法计算得到震源S2激发的地震波场的水平(a)和垂直(b)分量波场快照
Fig.7 The snapshots of the horizontal(a)and vertical(b)components of the excitation wavefield by Source 2 calculated respectively by M2 and M3 when t=0.4 s[JZ)]
模拟得到的接收器R1、R2记录的地震波合成波形水平和垂直分量如图 10所示。图 10a显示M2方法的模拟波形与参考波形(M3模拟结果)具有高度的一致性。图 10b显示,接收器R1和R2处的合成波形相对误差较小(最大波形误差约4%),说明当模型为非规则网格模型时,使用M2方法可得到精度较高的地震波模拟结果。[KG0.15mm]
为了说明δ函数离散形式的适用性,本文将2类δ函数离散形式进一步应用于FDM。FDM网格间隔为4 m(最短波长网格点数约为16),空间差分近似阶数为8阶。震源类型和模型参数与3.1节相同。
使用FDM模拟得到的合成波形如图 11a所示,图中显示使用M1和M2方法模拟得到的合成波形与解析波形具有较高的一致性。为了进一步对比2种方法的模拟结果精度,本文给出了接收器R1、R2的FDM合成波形相对误差。图 11b显示M2方法的模拟结果具有较高的精度(最大波形误差约为5%),但M1方法的模拟结果精度相对较低(最大波形误差约为8%)。说明在使用FDM开展地震波模拟时,使用M2方法处理震源可得到精度较高的模拟结果。
图8 震源为S2时,接收器R1、R2记录的SEM合成波形与参考波形(a)以及两者的相对误差(b)
Fig.8 The SEM synthetic and analytical waveforms of the Source 2-excited waveforms received by Receiver 1 and Receiver 2(a)and their relative errors(b)
综上,SEM和FDM均可使用M2方法处理点震源,说明M2方法不仅模拟精度高、适用性还广。
图 10 非均匀网格模型中接收器R1、R2的SEM合成波形与参考波形(a)以及两者的相对误差(b)
Fig.10 The SEM synthetic and analytical waveforms of the original waveforms received by Receiver 1 and Receiver 2(a)and their relative errors(b)in the irregular grid model
在数值模拟地震波传播时需要对震源项进行离散处理,震源函数的数学表达式通常包含δ函数,本文通过引入δ函数的离散形式可近似震源项。为了检验这种震源处理方式在SEM地震波模拟中的适用性,本文开展了多组数值算例进行检验。
数值算例表明,在SEM地震波模拟中使用δ函数的离散形式处理震源项可以得到精度较高的模拟结果。这种震源处理方式不仅适用于单极震源和矩张量震源,而且可以应用到非规则网格模型中的震源处理。本文提出的第二类δ函数离散形式模拟结果精度要高于第一类δ函数离散形式。此外,第二类δ函数离散形式不仅适用于SEM,也适用于其他数值模拟方法,例如FDM。
应该指出的是,δ函数离散形式也可用于有限破裂面条件下的震源近似。通过将有限破裂面离散成多个点源,然后采用δ函数离散形式近似各个点源,即可实现有限破裂面情形下的地震波场模拟。
附录A
式(8)中的矩阵和向量的具体形式为(Komatitsch,Tromp,1999,2002; 刘少林等,2021):
单元质量矩阵Me:
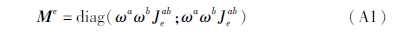
式中:ω表示GLL积分权; a、b表示单元GLL积分点的索引; J[KG*8]abe为单元雅可比矩阵在数值积分点(ξa1,ξb2)处行列式的值。
单元刚度矩阵Ke可表示为:

式中:
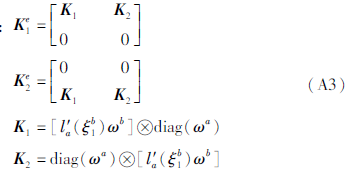
式中:为矩张量积运算符(Seriani,1997)。
向量Pe为:

式中:
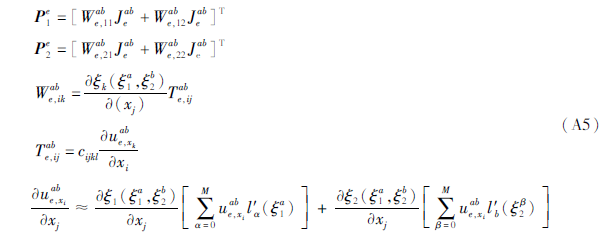
式中:cijkl为弹性张量; α、β表示单元GLL积分点的索引。
M3震源处理方法。通过散度定理和δ函数积分的积分性质可得:
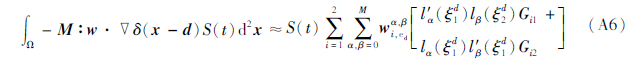
式中:ed为震源所在单元; G的表达式为:

式中:w为任意测试向量,根据w的任意性可得震源项的离散表达式为:
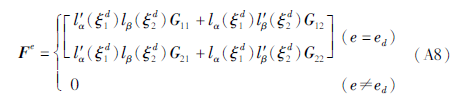
式(A8)即为式(9)的另一种离散形式。