第一作者简介:张 源(1981-),工程师,主要从事地震监测、前兆数据处理及形变资料应用研究.E-mail:371255488@qq.com.
通信作者简介:崔庆谷(1967-),正研级高级工程师,博士,主要从事地震观测研究.E-mail:3055366968@qq.com.
(1.云南省地震局 下关地震监测中心站,云南 大理 671000; 2.云南省地震局,云南 昆明 650224; 3.云南大理滇西北地壳构造活动中国地震局野外科学观测研究站,云南 大理 671000)
gPhone连续重力仪; 流动重力; 多项式; 小波滤波; 漂移修正
(1.Xiaguan Earthquake Monitoring Center Station of Yunnan Earthquake Agency,Dali 671000,Yunnan,China)(2.Yunnan Earthquake Agency,Kunming 650224,Yunnan,China)(3.Northwestern Yunnan Crustal Tectonics Observatory of CEA,Dali 671000,Yunnan,China)
continuous gravimeter gPhone; mobile gravity measurement; polynomials; wavelet filtering; drift correction
DOI: 10.20015/j.cnki.ISSN1000-0666.2025.0070
连续重力观测广泛应用于地球科学、环境科学、工程技术等领域的研究,通过对重力变化的监测与分析,可以捕捉到反映地球内部变化的高频信息(李响,2024),提升对地球动态过程的理解,进而为科研、资源管理及灾害预警提供支撑。重力场时变信号从性质上可以分为潮汐信号与非潮汐信号,其中潮汐信号占连续重力变化观测数 据 85%以上,其导致的短期重力变化可超过200 μGal(羊锴,韦进,2015),可以通过国际固体潮经验公式修正。非潮汐信号包含了仪器漂移和噪声、近场环境变化、近地表水循环、地球内部物质运移、构造作用引起的介质变形等多种信息(羊锴,韦进,2015)。仪器漂移分为线性漂移和非线性漂移,需要在获取有用信息前进行修正。线性漂移可根据时间直接修正,但非线性漂移如果缺乏有效约束,修正较为困难。
连续重力仪主要分为超导型和弹簧型,随着中国大陆构造环境监测网络项目的实施,截至2022年已经建设86个连续重力台站,并布设了106套弹簧型相对重力仪。非线性漂移是弹簧型连续重力仪的固有问题,阻碍了科研人员对重力非潮汐变化信号进行准确的分析和研究(韦进等,2011; 窦喜英等,2019)。因此,如何科学有效修正弹簧重力仪的非线性漂移是一个亟待解决的难题。目前主要采用台站绝对重力测量结果进行改正,但由于大部分台站并没有定期的绝对重力测量数据,因此这种方法无法大规模推广(王乐行等,2025)。国内外学者研究表明,利用多项式拟合方法可以较好地对弹簧重力仪的漂移进行修正(邢乐林等,2010; 马娟娟等,2024); 利用小波滤波对信号进行滤波去噪也可抑制漂移的影响(王乐行等,2025)。多项式拟合、小波滤波主要通过数据自洽性进行拟合,缺乏有效约束,修正后的数据与实际重力变化的契合度尚需进一步验证。
云龙地震台(下文简称“云龙台”)自2018以来获得多年的连续重力观测数据,且连续多年进行了绝对重力控制下的相对重力重复联测,获得年尺度重力值变化信息,为本文提供了新的思路。流动重力与连续重力2种观测物理同源,理论上其同时同址观测的重力变化量应该一致,因此可以采用流动观测的结果作为约束,对云龙台连续重力进行漂移修正,并将本文修正结果与多项式拟合、小波滤波等传统修正方法的结果进行对比,为连续重力仪漂移修正提供方法参考。
云龙台属于国家形变观测基本台,隶属于云南省地震局,位于怒江、澜沧江断裂系,处于龙陵、保山地震带及下关、丽江地震带之间(图1)。台站基底为侏罗纪细砂岩,且周围5 km范围内无机场、铁路、矿山石场、高压输电等因素影响,观测环境受周边干扰小。数十年观测资料表明云龙台具备优良的观测环境条件,其形变、测震、地磁等项目观测质量高(杨学慧等,2016)。2018年8月云龙台架设gPhone连续重力仪(编号X212MGPH0150)并试运行,2019年1月1日正式并入全国连续重力台网。该重力仪是美国Micro-g&Lacoste公司生产的零长弹簧系统相对重力仪,分辨率为0.1×10-8 m/s2,仪器具有高精度、高采样率、测程大等特点(周江林等,2015),其秒值观测资料给科研人员提供了丰富的地震信息(王林松等,2012)。
图2是经过Nakai检验得出的2019年1月—2024年5月云龙台重力仪M2波潮汐因子时间序列变化。65个月数据中,除5个月因仪器故障外,其余60个月的潮汐因子稳定在1.162~1.166,最大变化不足0.3%,且经过Nakai检验潮汐因子中误差都优于0.001。观测数据整体呈现相对平稳变化背景,仪器观测性能稳定,观测数据质量可靠。
连续重力观测数据gs主要由潮汐部分gt、非潮汐部分gn和误差ε组成,而非潮汐变化方面的gn由重力极潮gp、大气压负荷ga、陆地水负荷gw、仪器漂移gd和剩余误差ε1构成(韦进等,2012; 王乐行等,2025):
gs=gt+gn+ε (1)
gn=gp+ga+gw+gd+ε1 (2)
本文收集2019年1月1日—2024年5月31日云龙台gPhone连续重力仪原始观测数据(图3a),通过gMonitor软件预先设置经验参数,对原始资料中的重力极潮、大气压负荷、陆地水负荷等影响因素进行预处理和校正,每个月实时进行格值修正,并采用IERS(国际地球自转和参考系统服务)提供的潮汐模型(ETGTAB潮汐模式)来校正理论固体潮汐的影响(图3b)。
经整理后的数据还需要对地震、阶跃、人为干扰等异常值进行滤波处理,压制和剔除干扰信号,才能使非潮汐变化信号得到凸显。本文采用基于中值和中值绝对偏差(MAD)的Hampel滤波器来对数据作处理,相对于传统均值和标准差方法,Hampel滤波器通过使用中值和MAD提高异常值检测的准确性,识别并去除时间序列中的异常值。图3c是本文使用Hampel滤波器对数据异常值进行识别与剔除后的时间序列。
图3 云龙台重力原始值及预处理值时间序列
Fig.3 The time series of the original minute valuesof gravity recorded by Yunlong Station andtheir preprocessed ones
从图3可以看出,经去除固体潮汐、气压等因素后得到的连续重力预处理分钟值时间序列,大约以2021年4月为界分为2个阶段:第一阶段约2.3 a,观测值增长较快,总变化量约为1 189×10-8 m/s2,年速率约为517×10-8 m/s2; 第二阶段3.1 a,观测值增长明显变缓,总变化量约为184×10-8 m/s2,年速率约为59×10-8 m/s2; 第一阶段漂移率明显大于第二阶段; 从总的5.4 a连续观测数据变化趋势来看,仪器漂移较大,且非线性特征明显。
目前流动重力联测在云南的测点达到249个,其中包括9个绝对重力点,测段数为274段(刘东等,2021),平均点间距小于70 km,具有较好的空间分辨率,但是年均观测1~2期,时间分辨率不足; 而云南现有连续重力台站14个,空间分辨率不足,却可以达到秒级采样率,具有较好的时间分辨率。云南14个连续重力台站都进行了流动重力联测,采用本文的漂移率修正方法,可以在局部区域进行联合分析,弥补两者各自的不足。
云龙台周边有2个绝对重力观测台站,即丽江台及下关台,每年均进行绝对重力观测。云南省流动重力测量时,会将云龙台与2个绝对重力台站进行联测,结果如图4所示。联测过程采用CG-5型石英弹簧相对重力仪,采用A→B→C→……→C→B→A往返双程测量方法,并形成闭合环。通过去除漂移、固体潮等影响因素并平差解算后,获取云龙台基于2个绝对重力点控制下的重力值,
图4 云龙台与2个绝对重力台站联测
Fig.4 The joint observation network composed ofYunlong Station and other two absolute gravitystations:Xiaguan and Lijiang
相邻两期变化量视为云龙台该时段内的实际变化量。即相邻两期流动重力观测变化量gi,同时间段预处理连续重力仪观测变化量Gi(取该时段起止日期的日均值之差),Gi-gi为该时段内连续重力仪的漂移量。漂移量除以该时段总时长Ti(以分钟计算)即为该时段内的漂移率,通过该漂移率可以修正本时段内任何时刻观测量(分钟值)的漂移值。如下式所示:
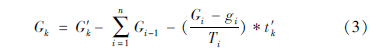
式中:Gk为第i时段内第k分钟的值; G'k为该时刻连续重力预处理值; Gi-1为i-1个时段漂移量的总和; 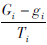 为第i时段的漂移率; t'k为时长; i为需要计算的时段,1≤i≤n且为整数,n为根据流动重力观测划分的总时段数。
为第i时段的漂移率; t'k为时长; i为需要计算的时段,1≤i≤n且为整数,n为根据流动重力观测划分的总时段数。
本文收集云南流动重力测网2018年第二期至2024年第二期观测资料,以2019年1月1日云龙台连续重力仪正式并网记录开始为第1期,视流动变化量g1与连续变化量G1都为0。从第2期开始,依次分别计算本阶流动变化量gi、连续变化量Gi以及漂移量Gi-gi,结果见表1。
通过式(3)及表1对连续重量预处理值进行计算,得出云龙台连续重力基于流动重力控制的5.4 a漂移修正结果,如图5所示。
表1 流动重力观测变化量与同时段连续重力观测变化量及差值
Tab.1 The variation of the mobile gravity observation and the variation of the continuous gravity observation in the same period and the difference between them
图5 基于流动重力控制的漂移修正分钟值时间序列
Fig.5 The time series of minute values after driftcorrection based on mobile gravity control
对比图3与图5可以看出,采用流动重力测量结果作为控制进行漂移修正后,连续重力整体变化趋势被有效压制,累计变化量从约1 374×10-8 m/s2降至69×10-8 m/s2,漂移修正后的时间序列显示出一定的起伏状态,该结果可能更接近构造运动或地下物质迁移引起的真实重力变化。为了检验本方法修正结果,后文将利用目前常用的多项式拟合和小波滤波方法进行对比分析。
多项式拟合方法是一种常用的非线性漂移改正方法,其优点是拟合后可消除数据大幅度的趋势性漂移影响,当阶次达到4阶后,漂移改正残差结果已趋于稳定(邢乐林等,2010; 韦进等,2012); 小波滤波是一种强大的信号处理工具,通过选择适当的小波基、分解和重构,可以有效地去除噪声或提取信号特征(王乐行等,2025)。本文选用5阶多项式及amor小波基对连续重力预处理值进行漂移修正,并与本文的流动重力控制修正结果对比,如图6所示。
由图6a可以看出:amor小波滤波方法修正结果平滑性较好,但起始和末尾阶段效果并不理想,与王乐行等(2025)研究结果呈现相同特征,趋势变化的数量级也远大于其它2种方法,不符合地质活动特征,这是由于小波滤波方法自身的边际效应所导致。图6b显示5阶多项式与本文流动重力控制修正后结果总体趋势一致,且与流动重力变化趋势基本相符,认为本文基于流动重力控制的漂移修正方法,能够有效去除gPhone弹簧重力仪的漂移趋势,达到目前公认的多项式修正漂移方法的水平,得到接近真实的重力非潮汐信号。
考虑到连续重力观测值的主要组成部分是潮汐分量,因此观测数据在理论上应与同一时间段内该观测站的理论固体潮汐模型具有较高的一致性。基于这一点,可将上述方法修正后的数据加回理论固体潮(图7),再将结果与理论固体潮作相关分析,以此评定各漂移修正方法的效果。从图7可以看出,基于流动重力控制、5阶多项式2种方法加回理论固体潮后,数据变化区间在±200×10-8 m/s2附近,主要表现为潮汐信号,流动重力控制方法的结果呈现出更多的波动信息。amor小波滤波的变化幅度较大,在(0~1 500)×10-8 m/s2内呈曲线型变化,这是源于本文数据时长5.4 a,小波滤波在处理长时间信号时容易引入边际效应,尤其是在信号的开头和结尾部分。
根据模型性能评估方法(王乐行等,2025; 马娟娟等,2024),从评估模型性能的均方根误差(RMSE)与决定系数(R2)2个指数(周鹏飞等,2024; 李永生等,2025)以及皮尔逊和斯皮尔曼等级相关系数进行对比,3种方法经过4种指标评定结果见表2。本文流动重力控制漂移修正方法的RMSE值为20.794 8,小于其他2种方法,该值越小表示模型的误差越小、性能越好; R2为0.907 3,是3种方法中最接近1的,表示模型解释数据方差比 例 最佳、解释能力最强; Pearson相关系数为0.975 01,是最接近1的,表示两个连续变量之间的线性关系最强; Spearman相关系数为0.972 08,也是最接近1的,表示2个变量之间的单调关系最强。可以看出,本文基于流动重力控制的漂移修正方法,各项指标均略优于5阶多项式,而amor小波滤波受边际效应影响,指标评价均不理想。
式(2)中连续重力仪非潮汐信号由重力极潮gp、大气压负荷ga、陆地水负荷gw、仪器漂移gd和残差ε1构成,残差包含观测误差和实际重力变化,残差分布检验也可对模型拟合程度进行检验。图8为3种方法残差分布情况,表3为残差分布统计,从图8和表3中可以看出,小波滤波方法由于边际效用,检验结果不理想; 基于流动重力控制方法和多项式拟合结果接近。多项式拟合的残差分布更接近于正态分布,偏度和标准差较小,缘于多项式是根据数据变化趋势进行拟合,拟合度较高,但部分实际重力变化也会被做为漂移处理; 基于流动重力控制方法时间分辨率不高,是根据观测时刻数据的校正,然后线性内插至时段内的任意时刻,对时段内的非线性漂移修正不完全。所以流动重力控制和多项式结果出现了偏锋不一致的情况。
仪器自身产生的长期非线性漂移量级远远超过了气压、极移、陆地水负荷以及构造活动等自然因素产生的重力变化。本文根据流动重力观测时刻对连续重力预处理值进行分段漂移修正,并与目前常用的漂移修正方法进行综合对比,得出以下结论:
(1)基于云龙台gPhone连续重力仪5.4 a的原始分钟值时间序列可以看出,仪器架设初期约2 a内,漂移率较大,之后漂移率逐渐减小,并趋于稳定。
(2)应用基于流动重力控制的漂移修正方法,对去除固体潮汐后的重力数据时间序列进行漂移修正后,5.4 a累计变化量从约1 374×10-8 m/s2降至69×10-8 m/s2,大幅度消除了漂移趋势性影响。
(3)基于流动重力控制方法与5阶多项式拟合方法的漂移修正结果总体趋势一致,但在细节上存在差异; 模型评价结果优于多项式拟合和小波滤波方法; 残差分布情况与多项式结果接近。
因观测数据的局限,本文方法尚有如下几个问题需要讨论和进一步研究:
(1)绝对重力与流动重力观测时间并不严格同步,但考虑到测网中绝对重力测点(大理、丽江)近年来变化较为稳定的特点,本文流动重力平差解算时未根据时差进行动态平差; 流动重力观测时刻的连续重力数据采用日均值,本文对于当天有地震或其他干扰的情况选择了前后3~5 d内较为稳定的日均值代替。观测数据的这2种处理方式对漂移修正结果会有微弱影响,但其影响量级有待进一步研究。
[HJ](2)本文方法的漂移修正结果与多项式拟合漂移改正结果均显示,在2021年5月21日漾濞MS6.4地震前约半年时间,重力观测曲线出现了明显的快速上升并急速转折下降的特征,是否为漾濞地震的震前异常,有待进一步研究。
(3)由于边际效用的影响,小波滤波漂移改正的方法是否适用于长周期的连续重力漂移修正尚待研究。
综上,基于流动重力控制的漂移修正方法,其修正结果能够达到目前学者们较为认可的多项式拟合修正水平,对弹簧型连续重力仪的漂移修正具有很好的参考价值,可以作为一种新的漂移修正思路推广应用。